
【题目】某学校举行数学竞赛,需购买![]() 两种奖品共160件,其中
两种奖品共160件,其中![]() 种奖品的单价为12元,
种奖品的单价为12元,![]() 种奖品的单价为8元,且购买
种奖品的单价为8元,且购买![]() 种奖品的数量不大于
种奖品的数量不大于![]() 种奖品数量的3倍,假设购买
种奖品数量的3倍,假设购买![]() 种奖品的数量为
种奖品的数量为![]() 件.
件.
(1)根据题意填空:
购买![]() 种奖品的费用为___(元);
种奖品的费用为___(元);
购买![]() 种奖品的费用为___(元);
种奖品的费用为___(元);
(2)若购买两种奖品所需的总费用为![]() 元,试求
元,试求![]() 与
与![]() 的函数关系式,并求出
的函数关系式,并求出![]() 的取值范围;
的取值范围;
(3)问![]() 两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
两种奖品各购买多少件时所需的总费用最少,并求出最少费用.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)购买
;(3)购买![]() 种奖品40件,
种奖品40件,![]() 种奖品120件时,所需费用最少,最少费用为1440元.
种奖品120件时,所需费用最少,最少费用为1440元.
【解析】
(1)根据总费用=单价×数量填空;
(2)根据题意可以写出y与x的函数关系式,根据题意可以列出相应的不等式,求出x的取值范围;
(3)根据一次函数的性质即可解答本题.
解:(1)根据题意填空:
购买![]() 种奖品的费用为
种奖品的费用为 ![]() (元);
(元);
购买![]() 种奖品的费用为
种奖品的费用为![]() (元);
(元);
(2)根据题意得,![]()
∴![]()
![]() ,解得:
,解得:![]()
由题意得:![]()
∴![]() ;
;
(3)∵![]()
∴![]() 随
随![]() 的增大而增大
的增大而增大
∵![]()
∴当![]() 时,
时,![]() (元)
(元)
![]()
∴当购买![]() 种奖品40件,
种奖品40件,![]() 种奖品120件时,所需费用最少,最少费用为1440元 .
种奖品120件时,所需费用最少,最少费用为1440元 .
故答案为:(1)![]() ,
,![]() ;(2)
;(2)![]() ,
,![]() ;(3)购买
;(3)购买![]() 种奖品40件,
种奖品40件,![]() 种奖品120件时,所需费用最少,最少费用为1440元.
种奖品120件时,所需费用最少,最少费用为1440元.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
【题目】出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:![]() )如下:
)如下:
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
问:(1)将最后一位乘客送到目的地时,小李在什么位置?
(2)若汽车耗油量为![]() (升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为![]() (包括
(包括![]() ),超过部分每千米1.2元,问小李这天上午共得车费多少元?
),超过部分每千米1.2元,问小李这天上午共得车费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D是BC上一点,DE∥AB,交AC于点E,DF∥AC,交AB点F.

(1)直接写出图中与∠BAC构成的同旁内角.
(2)请说明∠A与∠EDF相等的理由.
(3)若∠BDE +∠CDF=234°,求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小张骑自行车匀速从甲地到乙地,在途中休息了-段时间后,仍按原速行驶他距乙地的距离与时间的关系如图中折线所示,小李骑摩托车匀速从乙地到甲地,比小张晚出发一段时间,他距乙地的距离与时间的关系如图中线段AB所示,
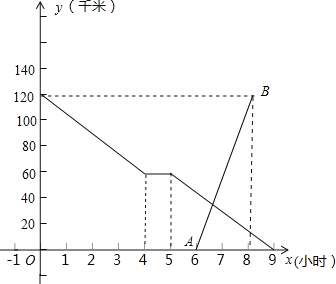
(1)小李到达甲地后,再经过 小时小张到达乙地;小张骑自行车的速度是 千米/小时;
(2)请你写出小李距乙地的距离y(千米)与时间x(小时)之间的函数关系(不要求写出定义域);
(3)若小李想在小张休息期间(第4小时和第5小时不算小张休息)与他相遇,则他出发的时间x应在什么范围?(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:数学课上,吴老师在求代数式x2﹣4x+5的最小值时,利用公式a2±2ab+b2=(a±b)2,对式子作如下变形:x2﹣4x+5=x2﹣4x+4+1=(x﹣2)2+1,
因为(x﹣2)2≥0,
所以(x﹣2)2+1≥1,
当x=2时,(x﹣2)2+1=1,
因此(x﹣2)2+1有最小值1,即x2﹣4x+5的最小值为1.
通过阅读,解下列问题:
(1)代数式x2+6x+12的最小值为 ;
(2)求代数式﹣x2+2x+9的最大或最小值;
(3)试比较代数式3x2﹣2x与2x2+3x﹣7的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读并回答问题.
求一元二次方程ax2+bx+c=0(a≠0)的根(用配方法).
解:ax2+bx+c=0,
∵a≠0,∴x2+![]() x+
x+![]() =0,第一步
=0,第一步
移项得:x2+![]() x=﹣
x=﹣![]() ,第二步
,第二步
两边同时加上(![]() )2,得x2+
)2,得x2+![]() x+( )2=﹣
x+( )2=﹣![]() +(
+(![]() )2,第三步
)2,第三步
整理得:(x+![]() )2=
)2=![]() 直接开方得x+
直接开方得x+![]() =±
=±![]() ,第四步
,第四步
∴x=![]() ,
,
∴x1=![]() ,x2=
,x2=![]() ,第五步
,第五步
上述解题过程是否有错误?若有,说明在第几步,指明产生错误的原因,写出正确的过程;若没有,请说明上述解题过程所用的方法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB=90°,BD是△ABC的角平分线,P是射线AC上任意一点 (不与A. D. C三点重合),过点P作PQ⊥AB,垂足为Q,交直线BD于E.

(1)如图①,当点P在线段AC上时,说明∠PDE=∠PED.
(2)作∠CPQ的角平分线交直线AB于点F,则PF与BD有怎样的位置关系?画出图形并说明理由。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面的文字,解答问题:大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,而
的小数部分我们不可能全部写出来,而![]() <2于是可用
<2于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是_______,小数部分是_________;
的整数部分是_______,小数部分是_________;
(2)如果![]() 的小数部分为
的小数部分为![]() 的整数部分为
的整数部分为![]() 求
求![]() 的值;
的值;
(3)已知:![]() 其中
其中![]() 是整数,且
是整数,且![]() 求
求![]() 的平方根。
的平方根。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com