
【题目】如图,D是BC上一点,DE∥AB,交AC于点E,DF∥AC,交AB点F.

(1)直接写出图中与∠BAC构成的同旁内角.
(2)请说明∠A与∠EDF相等的理由.
(3)若∠BDE +∠CDF=234°,求∠BAC的度数.
科目:初中数学 来源: 题型:
【题目】某采摘农场计划种植![]() 两种草莓共6亩,根据表格信息,解答下列问题:
两种草莓共6亩,根据表格信息,解答下列问题:

(1)若该农场每年草莓全部被采摘的总收入为![]() 元,那么
元,那么![]() 两种草莓各种多少亩? (2)若要求种植
两种草莓各种多少亩? (2)若要求种植![]() 种草莓的亩数不少于种植
种草莓的亩数不少于种植![]() 种草莓的一半,那么种植
种草莓的一半,那么种植![]() 种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?
种草莓多少亩时,可使该农场每年草莓全部被采摘的总收入最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
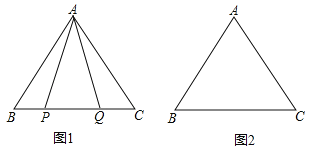
【题目】在等边△ABC中:
(1)如图1,P,Q是BC边上的两点,AP=AQ,∠BAP=20°,求∠AQB的度数;
(2)点P,Q是BC边上的两个动点(不与点B,C重合),点P在点Q的左侧,且AP=AQ,点Q关于直线AC的对称点为M,连接AM,PM.
①依题意将图2补全;
②小茹通过观察、实验提出猜想:在点P,Q运动的过程中,始终有PA=PM,小茹把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:要证明PA=PM,只需证△APM是等边三角形;
想法2:在BA上取一点N,使得BN=BP,要证明PA=PM,只需证△ANP≌△PCM;
想法3:将线段BP绕点B顺时针旋转60°,得到线段BK,要证PA=PM,只需证PA=CK,PM=CK…
请你参考上面的想法,帮助小茹证明PA=PM(一种方法即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线BD经过坐标原点O,矩形的边分别平行于坐标轴,反比例函数![]() (k>0)的图象分别与BC、CD交于点M、N.若点A(-2,-2),且△OMN的面积为
(k>0)的图象分别与BC、CD交于点M、N.若点A(-2,-2),且△OMN的面积为![]() ,则k=( )
,则k=( )
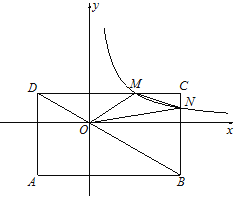
(A)2.5 (B)2 (C)1.5 (D)1
查看答案和解析>>
科目:初中数学 来源: 题型:
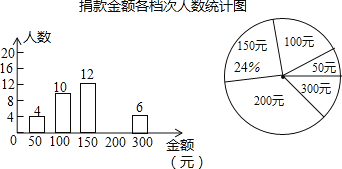
【题目】企业举行“爱心一日捐”活动,捐款金额分为五个档次,分别是50元,100元,150元,200元,300元.宣传小组随机抽取部分捐款职工并统计了他们的捐款金额,绘制成两个不完整的统计图,请结合图表中的信息解答下列问题:
(1)宣传小组抽取的捐款人数为_____人,请补全条形统计图;
(2)在扇形统计图中,求100元所对应扇形的圆心角的度数;
(3)已知该企业共有500人参与本次捐款,请你估计捐款总额大约为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校根据课程设置要求,开设了数学类拓展性课程.为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整).请根据图中信息回答问题:

(1)求![]() 的值;
的值;
(2)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明每天早上7:30从家出发,到距家![]() 的学校上学,一天,小明以
的学校上学,一天,小明以![]() 的速度上学,
的速度上学,![]() 后小明爸爸发现他发现忘带语文书,爸爸立即带上语文书去追赶小明.
后小明爸爸发现他发现忘带语文书,爸爸立即带上语文书去追赶小明.
(1)如果爸爸以![]() 的速度追小明,爸爸追上小明时距离学校多远?
的速度追小明,爸爸追上小明时距离学校多远?
(2)如果爸爸刚好能在学校门口追上小明,爸爸的速度是多少?
(3)爸爸以![]() 的速度追赶小明,他把书给小明后及时原路原速返回(交书耽误的时间忽略不计),返回家的时间是多少?
的速度追赶小明,他把书给小明后及时原路原速返回(交书耽误的时间忽略不计),返回家的时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一销售员向某企业推销一种该企业生产必需的物品,若企业要40件,则销售员每件可获利40元,销售员(在不亏本的前提下)为扩大销售量,而企业为了降低生产成本,经协商达成协议,如果企业购买40件以上时,每多要1件,则每件降低1元.
(1)设每件降低![]() (元)时,销售员获利为
(元)时,销售员获利为![]() (元),试写出
(元),试写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当每件降低20元时,问此时企业需购进物品多少件?此时销售员的利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com