【题目】一销售员向某企业推销一种该企业生产必需的物品，若企业要40件，则销售员每件可获利40元，销售员（在不亏本的前提下）为扩大销售量，而企业为了降低生产成本，经协商达成协议，如果企业购买40件以上时，每多要1件，则每件降低1元．
（1）设每件降低
（元）时，销售员获利为
（元），试写出关于的函数关系式．
（2）当每件降低20元时，问此时企业需购进物品多少件？此时销售员的利润是多少？
【答案】（1）
；（2）企业购进60件，销售员利润1200元.
【解析】
（1）根据题意每件降低x元时代表企业在40件的基础上多要x件，而此时销售员每件可获利为40-x，由获利=件数
每件获利即可得关系式 ；
（2）每件降低20元，证明在40件的基础上多要20件，再代入（1）的关系式可得销售员此时获利.
解：（1）根据题意每件降低x元时代表企业在40件的基础上多要x件，而此时销售员每件可获利为40-x，则销售员可获利：
，
因题意规定销售员为不亏本的前提，所以自变量
，
综上可知函数关系式为；
（2）每件降低20元，证明在40件的基础上多要20件，即此时企业需要购进60件，
根据（1）的关系式，当x=20时，销售员获利
.
优质课堂快乐成长系列答案科目：初中数学 来源： 题型：
【题目】如图，D是BC上一点，DE∥AB，交AC于点E，DF∥AC，交AB点F．
（1）直接写出图中与∠BAC构成的同旁内角．
（2）请说明∠A与∠EDF相等的理由．
（3）若∠BDE +∠CDF＝234°，求∠BAC的度数．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（
，0），且与y轴相交于点C．
（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】定义：只有一组对角是直角的四边形叫做损矩形，连结它的两个非直角顶点的线段叫做这个损矩形的直径．
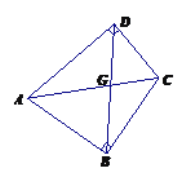
（1）如图，损矩形
中，
，则该损矩形的直径是线段______．
（2）探究：在上述损矩形内，是否存在点
，使
四个点都在以为圆心的同一圆上，若存在，请指出点的具体位置___________________________；若不存在，请说明理由.
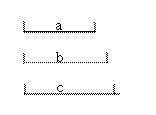
（3）实践：已知如图三条线段
，求作相邻三边长顺次为的损矩形（尺规作图，保留作图痕迹）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着－5，－2，1，9，且任意相邻四个台阶上数的和都相等.
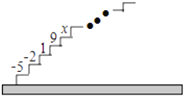
（尝试）（1）求前4个台阶上数的和是多少？
（2）求第5个台阶上的数
是多少？
（应用）求从下到上前33个台阶上数的和.
（发现）试用含
（为正整数）的式子表示出数“－2”所在的台阶数（此问直接写出结果）.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如下图中的小正方形的大小相等，图1只有一个小正方形；图2是由4个小正方形构成的一个正方形；图3是由9个小正方形构成的一个正方形，…以此类推，每一个图形都是由小正方形构成的大正方形. 回答下列问题：
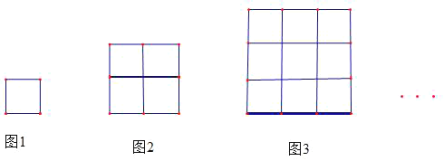
（1）图2比图1多________个小正方形，图3比图2多________个小正方形.
（2）图
比图
多________个小正方形（用含的式子表示）
（3）猜想
________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某校初三（1）班50名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 | a |
一分钟跳绳 | 8 | 0.16 |
投掷实心球 | b | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
（1）求a，b的值；
（2）若将各自选项目的人数所占比例绘制成扇形统计图，求“一分钟跳绳”对应扇形的圆心角的度数；
（3）在选报“推铅球”的学生中，有3名男生，2名女生，为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，求所抽取的两名学生中至多有一名女生的概率．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
