
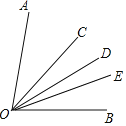
【题目】如图,∠DOE:∠BOE=1:2,∠AOC:∠DOC=2:1,如果∠AOB=87°,那么∠COE=_____.
【答案】29°
【解析】
由∠DOE:∠BOE=1:2,∠AOC:∠DOC=2:1,可设∠DOE=x°,∠DOC=y°,可得∠BOE=2x°,∠AOC=2y°,然后根据∠AOB=87°,可得∠DOE+∠BOE+∠DOC+∠AOC=∠AOB=87°,可求x+y的度数,即可求∠COE的度数.
解:设∠DOE=x°,∠DOC=y°,
∵∠DOE:∠BOE=1:2,∠AOC:∠DOC=2:1,
∴∠BOE=2x°,∠AOC=2y°,
∵∠DOE+∠BOE+∠DOC+∠AOC=∠AOB,
∴x°+2x°+y°+2y°=87°,
∴3(x°+y°)=87°,
∴x°+y°=29,
∵∠COE=∠DOE+∠DOC
∴∠COE=x°+y°=29°.
故答案为:29°


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】某校根据课程设置要求,开设了数学类拓展性课程.为了解学生最喜欢的课程内容,随机抽取了部分学生进行问卷调查(每人必须且只选其中一项),并将统计结果绘制成如下统计图(不完整).请根据图中信息回答问题:

(1)求![]() 的值;
的值;
(2)补全条形统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
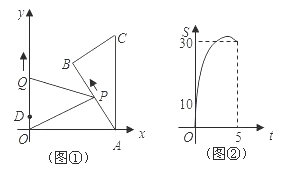
【题目】如图①,Rt△ABC中,∠B=90°,∠CAB=30°,它的顶点A的坐标为(10,0),顶点B的坐标为(5,5![]() ),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
),AB=10,点P从点A出发,沿A→B→C的方向匀速运动,同时点Q从点D(0,2)出发,沿y轴正方向以相同速度运动,当点P到达点C时,两点同时停止运动,设运动的时间为t秒.
(1)当点P在AB上运动时,△OPQ的面积S(平方单位)与时间t(秒)之间的函数图象为抛物线的一部分,(如图②),则点P的运动速度为 ;
(2)求(1)中面积S与时间t之间的函数关系式及面积S的最大值及S取最大值时点P的坐标;
(3)如果点P,Q保持(1)中的速度不变,那么点P沿AB边运动时,∠OPQ的大小随着时间t的增大而增大;沿着BC边运动时,∠OPQ的大小随着时间t的增大而减小,当点P沿这两边运动时,使∠OPQ=90°的点P有 个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一销售员向某企业推销一种该企业生产必需的物品,若企业要40件,则销售员每件可获利40元,销售员(在不亏本的前提下)为扩大销售量,而企业为了降低生产成本,经协商达成协议,如果企业购买40件以上时,每多要1件,则每件降低1元.
(1)设每件降低![]() (元)时,销售员获利为
(元)时,销售员获利为![]() (元),试写出
(元),试写出![]() 关于
关于![]() 的函数关系式.
的函数关系式.
(2)当每件降低20元时,问此时企业需购进物品多少件?此时销售员的利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
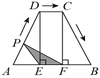
【题目】如图,梯形ABCD中,AB∥DC,DE⊥AB,CF⊥AB,且AE=EF=FB=5,DE=12动点P从点A出发,沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒,y=![]() ,则y与t的函数图象大致是()
,则y与t的函数图象大致是()
A.  B.
B. 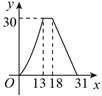 C.
C. 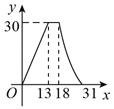 D.
D. 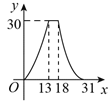
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象都经过点A(m,2).
)的图象都经过点A(m,2).

(1)求点A的坐标及反比例函数的表达式;
(2)设一次函数![]() 的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
的图象与x轴交于点B,若点P是x轴上一点,且满足△ABP的面积是2,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明用的练习本可以到甲商店购买,也可以到乙商店购买,已知两商店的标价都是每本1元,甲商店的优惠条件是:购买10本以上,从第11本开始按标价的70%卖;乙商店的优惠条件是:每本按标价的80%卖.
(1)小明要买20本时,到哪个商店较省钱?
(2)买多少本时到两个商店付的钱一样?
(3)小明现有32元钱,最多可买多少本?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据图中给出的信息,解答下列问题:
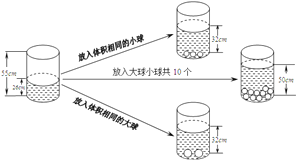
(1)放入一个小球水面升高 ,![]() ,放入一个大球水面升高
,放入一个大球水面升高 ![]() ;
;
(2)如果要使水面上升到50![]() ,应放入大球、小球各多少个?
,应放入大球、小球各多少个?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com