练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】根据图中给出的信息，解答下列问题：

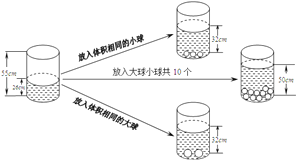
    （1）放入一个小球水面升高 ，，放入一个大球水面升高 ；

    （2）如果要使水面上升到50，应放入大球、小球各多少个？

    【答案】详见解析

    【解析】

    （1）设一个小球使水面升高x厘米，一个大球使水面升高y厘米，根据图象提供的数据建立方程求解即可。

    （2）设应放入大球m个，小球n个，根据题意列一元二次方程组求解即可。

    解：（1）设一个小球使水面升高x厘米，由图意，得3x=32﹣26，解得x=2。

    设一个大球使水面升高y厘米，由图意，得2y=32﹣26，解得：y=3。

    所以，放入一个小球水面升高2cm，放入一个大球水面升高3cm。

    （2）设应放入大球m个，小球n个，由题意，得

    ，解得：。

    答：如果要使水面上升到50cm，应放入大球4个，小球6个。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，∠DOE：∠BOE＝1：2，∠AOC：∠DOC＝2：1，如果∠AOB＝87°，那么∠COE＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

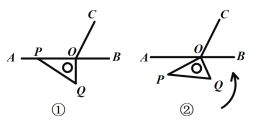
    【题目】如图①，为直线上一点，作射线，使，将一个直角三角尺如图摆放，直角顶点在点处，一条直角边在射线上. 将图中的三角尺绕点以每秒10°的速度按逆时针方向旋转（如图②所示），在旋转一周的过程中，第秒时，所在直线恰好平分，则的值为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校初三（1）班50名学生需要参加体育“五选一”自选项目测试，班上学生所报自选项目的情况统计表如下：

    自选项目

    人数

    频率

    立定跳远

    9

    0.18

    三级蛙跳

    12

    a

    一分钟跳绳

    8

    0.16

    投掷实心球

    b

    0.32

    推铅球

    5

    0.10

    合计

    50

    1

    （1）求a，b的值；

    （2）若将各自选项目的人数所占比例绘制成扇形统计图，求“一分钟跳绳”对应扇形的圆心角的度数；

    （3）在选报“推铅球”的学生中，有3名男生，2名女生，为了了解学生的训练效果，从这5名学生中随机抽取两名学生进行推铅球测试，求所抽取的两名学生中至多有一名女生的概率．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

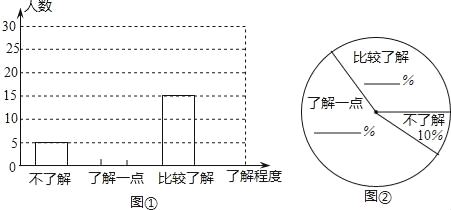
    【题目】某校八年级共有800名学生，准备调查他们对“低碳”知识的了解程度．

    （1）在确定调查方式时，团委设计了以下三种方案：

    方案一：调查八年级部分女生；

    方案二：调查八年级部分男生；

    方案三：到八年级每个班去随机调查一定数量的学生．

    请问其中最具有代表性的一个方案是_____；

    （2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图（如图①、图②所示），请你根据图中信息，将两个统计图补充完整；

    （3）请你估计该校八年级约有多少名学生比较了解“低碳”知识．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

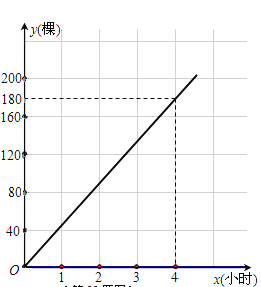
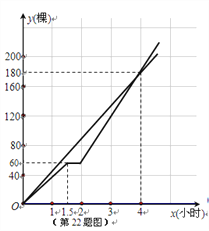
    【题目】为了“绿化环境，美化家园”，3月12日（植树节）上午8点，某校901、902班同学同时参加义务植树．901班同学始终以同一速度种植树苗，种植树苗的棵数y1与种植时间x(小时)的函数图象如图所示；902班同学开始以1小时种植40棵的速度工作了1.5小时后，因需更换工具而停下休息半小时，更换工具后种植速度提高至原来的1.5倍.

    （1）求902班同学上午11点时种植的树苗棵数；

    （2）分别求出901班种植数量y1、902班种植数量y2与种植时间x（小时）之间的函数关系式，并在所给坐标系上画出y2关于x的函数图象；

    （3）已知购买树苗不多于120棵时，每棵树苗的价格是20元；购买树苗超过120棵时，超过的部分每棵价格17元.若本次植树所购树苗的平均成本是18元，则两班同学上午几点可以共同完成本次植树任务？

    【答案】（1）120棵；（2）见解析；（3）两班同学上午12点可以共同完成本次植树任务.

    【解析】分析：直接进行计算即可.

    用待定系数法求一次函数解析式即可, 902班的要分成3段.

    当x=2时，两班同学共植树150棵，平均成本：不符合题意；，x>2，两班共植树（105x-60）棵.列出方程 求解即可.

    详解：（1）902班同学上午11点时种植的树苗棵数为：

    （棵）

    （2）由图可知，y1是关于x的正比例函数，可设y1=k1x，经过（4，180），

    代入可得

    ∴（x≥0）,

    ,

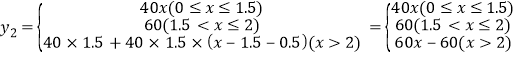    y2关于x的函数图象如图所示.

    （3）当x=2时，两班同学共植树150棵，

    平均成本：

    所以，x>2，两班共植树（105x-60）棵.

    由题意可得：

    解得：x=4.

    ,

    所以，两班同学上午12点可以共同完成本次植树任务.

    点睛：考查了待定系数法求一次函数解析式，一元一次方程的应用，注意分类讨论

    的数学思想方法.

    【题型】解答题
    【结束】
    23

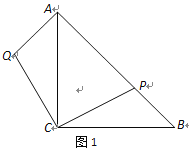
    【题目】在等腰直角△ABC中，，AC=BC，点P在斜边AB上（AP>BP）.作AQ⊥AB，且AQ=BP，连结CQ（如图1）.

    （1）求证：△ACQ≌△BCP；

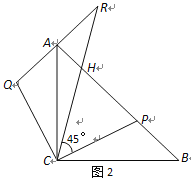
    （2）延长QA至点R，使得∠RCP=45°，RC与AB交于点H，如图2.

    ①求证：CQ2=QA·QR ；

    ②判断三条线段AH、HP、PB的长度满足的数量关系，并说明理由.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】特殊两位数乘法的速算——如果两个两位数的十位数字相同，个位数字相加为10，那么能立说出这两个两位数的乘积.如果这两个两位数分别写作AB和AC（即十位数字为A，个位数字分别为B、C，B+C=10，A>3），那么它们的乘积是一个4位数，前两位数字是A和(A+1)的乘积，后两位数字就是B和C的乘积.

    如：47×43=2021，61×69=4209.

    （1）请你直接写出83×87的值；

    （2）设这两个两位数的十位数字为x(x>3)，个位数字分别为y和z（y+z=10)，通过计算验证这两个两位数的乘积为100x(x+1)+yz.

    （3）99991×99999=___________________（直接填结果）

    【答案】7221

    【解析】分析：套用上面的归纳总结代入数据，即可得出结论；

    利用上面总结的结论套入数据表示出该两个两位数的成绩，在将等式展开合并同类项得出左边=右边，从而证明结论成立．

    直接运算即可.

    详解：(1)83和87满足题中的条件，即十位数都是8,8>3,且个位数字分别是3和7，之和为10,那么它们的乘积是一个4位数，前两位数字是8和9的乘积，后两位数字就是3和7的乘积，因而，答案为：7221.

    (2) 这两个两位数的十位数字为x(x>3)，个位数字分别为y和z，则由题知y+z=10,

    因而有：(10x+y)(10x+z)=100x2+10xz+10xy+yz

    =100x2+10x(y+z)+yz,

    =100x2+100x+yz,

    =100x(x+1)+yz.

    （3）9999000009.

    点睛：通过阅读题干掌握题中所给信息得出推理方法，然后通过多项式的展开式得出答案.学生应熟练掌握归纳推理的数学思想.

    【题型】解答题
    【结束】
    19

    【题目】为了大力弘扬和践行社会主义核心价值观，某乡镇在一条公路旁的小山坡上，树立一块大型标语牌AB，如图所示，标语牌底部B点到山脚C点的距离BC为20米，山坡的坡角为30°． 某同学在山脚的平地F处测量该标语牌的高，测得点C到测角仪EF的水平距离CF = 1.7米，同时测得标语牌顶部A点的仰角为45°，底部B点的仰角为20°，求标语牌AB的高度．（参考数值：sin20°≈0.34，cos20°≈0.94，tan20°≈0.36，）

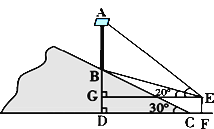
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，数轴上有两定点A、B，点表示的数为6，点B在点A的左侧，且AB=20，动点P从点A出发，以每秒4个单位长度的速度沿数轴向左匀速运动，设运动时间为t秒（t>0）.

    （1）写出数轴上点B表示的数______，点P表示的数用含t的式子表示：_______；

    （2）设点M是AP的中点，点N是PB的中点.点P在直线AB上运动的过程中，线段MN的长度是否会发生变化？若发生变化，请说明理由；若不变化，求出线段MN的长度.

    （3）动点R从点B出发，以每秒2个单位长度的速度沿数轴向左匀速运动，若点P、R同时出发；当点P运动多少秒时？与点R的距离为2个单位长度.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，点为平面内一点.

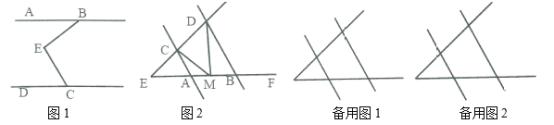
    （1）如图1，和互余，小明说过作，很容易说明。请帮小明写出具体过程；

    （2）如图2，，当点在线段上移动时（点与，两点不重合），指出与，的数量关系？请说明理由；

    （3）在（2）的条件下，若点在，两点外侧运动（点与，，三点不重合）请直接写出与，的数量关系.

    查看答案和解析>>

    同步练习册答案