
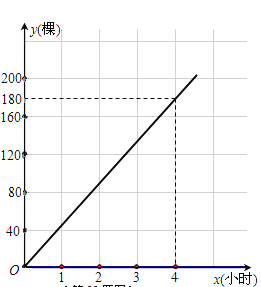
����Ŀ��Ϊ�ˡ��̻�����������������3��12�գ�ֲ���ڣ�����8�㣬ijУ901��902��ͬѧͬʱ�μ�����ֲ����901��ͬѧʼ����ͬһ�ٶ���ֲ��������ֲ����Ŀ���y1����ֲʱ��x(Сʱ)�ĺ���ͼ����ͼ��ʾ��902��ͬѧ��ʼ��1Сʱ��ֲ40�õ��ٶȹ�����1.5Сʱ������������߶�ͣ����Ϣ��Сʱ���������ߺ���ֲ�ٶ������ԭ����1.5��.
��1����902��ͬѧ����11��ʱ��ֲ�����������
��2���ֱ����901����ֲ����y1��902����ֲ����y2����ֲʱ��x��Сʱ��֮��ĺ�����ϵʽ��������������ϵ�ϻ���y2����x�ĺ���ͼ��
��3����֪�������粻����120��ʱ��ÿ������ļ۸���20Ԫ���������糬��120��ʱ�������IJ���ÿ�ü۸�17Ԫ.������ֲ�����������ƽ���ɱ���18Ԫ��������ͬѧ���缸����Թ�ͬ��ɱ���ֲ������
���𰸡���1��120�ã���2������������3������ͬѧ����12����Թ�ͬ��ɱ���ֲ������.
��������������![]() ֱ�ӽ��м��㼴��.
ֱ�ӽ��м��㼴��.
![]() �ô���ϵ������һ�κ�������ʽ����, 902���Ҫ�ֳ�3��.
�ô���ϵ������һ�κ�������ʽ����, 902���Ҫ�ֳ�3��.
![]() ��x=2ʱ������ͬѧ��ֲ��150�ã�
��x=2ʱ������ͬѧ��ֲ��150�ã�![]() ƽ���ɱ������������⣻��x>2�����ֲ����105x-60����.�г�����
ƽ���ɱ������������⣻��x>2�����ֲ����105x-60����.�г�����![]() ��⼴��.
��⼴��.
��⣺��1��902��ͬѧ����11��ʱ��ֲ���������Ϊ��
![]() ���ã�
���ã�
��2����ͼ��֪��y1�ǹ���x������������������y1=k1x��������4��180����
����ɵ�![]()
��![]() ��x��0��,
��x��0��,
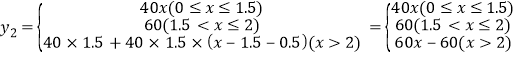 ,
,
y2����x�ĺ���ͼ����ͼ��ʾ.
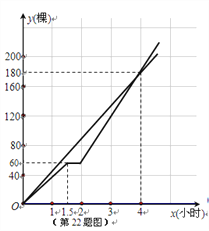
��3����x=2ʱ������ͬѧ��ֲ��150�ã�
![]() ƽ���ɱ���
ƽ���ɱ���
���ԣ�x>2�����ֲ����105x-60����.
![]() ������ɵã�
������ɵã�
��ã�x=4.
![]() ,
,
���ԣ�����ͬѧ����12����Թ�ͬ��ɱ���ֲ������.
�㾦�������˴���ϵ������һ�κ�������ʽ��һԪһ�η��̵�Ӧ�ã�ע���������
����ѧ˼�뷽��.
�����͡������
��������
23
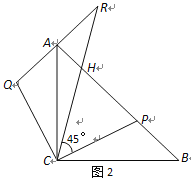
����Ŀ���ڵ���ֱ�ǡ�ABC�У���AC=BC����P��б��AB�ϣ�AP>BP��.��AQ��AB����AQ=BP������CQ����ͼ1��.
��1����֤����ACQ����BCP��
��2���ӳ�QA����R��ʹ�á�RCP=45�㣬RC��AB���ڵ�H����ͼ2.
����֤��CQ2=QA��QR ��
���ж������߶�AH��HP��PB�ij��������������ϵ����˵������.
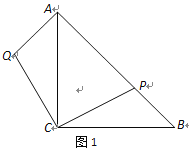
���𰸡�������
��������������![]() ֤��
֤��![]() ����
����![]() ����֤����ACQ����BCP.
����֤����ACQ����BCP.
![]() �ٸ�������Ƕ�Ӧ��ȵ���������������֤����CQR����AQC���������������εĶ�Ӧ�߳ɱ����õ�
�ٸ�������Ƕ�Ӧ��ȵ���������������֤����CQR����AQC���������������εĶ�Ӧ�߳ɱ����õ�![]() ����֤��.
����֤��.
������QH��֤����QCH����PCH���õ�HQ=HP. ��![]() �У��ù��ɶ������ɵõ�AH��HP��PB��������ϵ.
�У��ù��ɶ������ɵõ�AH��HP��PB��������ϵ.
��⣺��1����![]()
��![]()
�֡�AQ��AB,
��![]()
����ACQ����BCP��
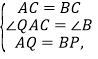
������ACQ����BCP (SAS)
��2�����ɣ�1��֪��ACQ����BCP����![]()
��![]() ��RCP=45�㣬
��RCP=45�㣬
���ACR+��PCB=45��,
�����ACR+��QCA =45�㣬
����QCR =45��=��QAC ,
���֡�QΪ�����ǣ�
����CQR����AQC��
![]()
��CQ2=QA��QR.
��![]() .
.
���ɣ�����QH���ɣ�1����2����֪��![]() ��CQ=CP.
��CQ=CP.
��CH ����QCH����PCH�Ĺ����ߣ�
���QCH����PCH��SAS��.
��HQ=HP.
��![]() ��
��![]() ��
��
���ɣ�1��֪��QA=PB��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ�κ���![]() ��ͼ���뷴��������
��ͼ���뷴��������![]() ��
��![]() ��������
Ϊ��������![]() ����ͼ������A��m��2����
����ͼ������A��m��2����

��1�����A�����꼰�����������ı���ʽ��
��2����һ�κ���![]() ��ͼ����x�ύ�ڵ�B������P��x����һ�㣬��������ABP�������2��ֱ��д����P��������
��ͼ����x�ύ�ڵ�B������P��x����һ�㣬��������ABP�������2��ֱ��д����P��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������![]() ��
��![]() ��
��![]() ���㣬�������¶��壺������һ����������������ľ���ǡ������2����������ϵ����Ƹõ������������������������.���������ϵ�
���㣬�������¶��壺������һ����������������ľ���ǡ������2����������ϵ����Ƹõ������������������������.���������ϵ�![]() ��
��![]() ��
��![]() ����ʾ�����ֱ�Ϊ1, 3��4����ʱ��
����ʾ�����ֱ�Ϊ1, 3��4����ʱ��![]() �ǵ�
�ǵ�![]() ��
��![]() ������������.
������������.
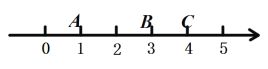
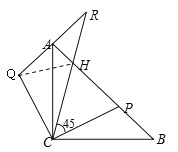
��1������![]() ��ʾ��-2����
��ʾ��-2����![]() ��ʾ��1�����и���-1, 2, 4, 6����Ӧ�ĵ�ֱ���
��ʾ��1�����и���-1, 2, 4, 6����Ӧ�ĵ�ֱ���![]() ,
,![]() ��
��![]() ��
��![]() �������ǵ�
�������ǵ�![]() ��
��![]() ����������������
����������������
��2����![]() ��ʾ��-10����
��ʾ��-10����![]() ��ʾ��15��
��ʾ��15��![]() Ϊ������һ�����㣺
Ϊ������һ�����㣺
������![]() �ڵ�
�ڵ�![]() ����࣬�ҵ�
����࣬�ҵ�![]() �ǵ�
�ǵ�![]() ��
��![]() �����������������ʱ��
�����������������ʱ��![]() ��ʾ������
��ʾ������
������![]() �ڵ�
�ڵ�![]() ���Ҳ࣬��
���Ҳ࣬��![]() ��
��![]() ��
��![]() �У���һ����ǡ�����������������������������ֱ��д����ʱ��
�У���һ����ǡ�����������������������������ֱ��д����ʱ��![]() ��ʾ����.
��ʾ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
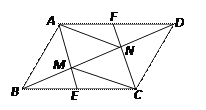
����Ŀ����ͼ������ABCD�У�E��F�ֱ�ΪBC��AD���е㣬AE��CF�ֱ�BD�ڵ�M��N�����ı��� AMCN����ABCD�������Ϊ�� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
���𰸡�B
������������������ƽ���ı���һ����ͶԱ��е������һ�����ȷ�ƽ���ı��ε�һ�Խ��ߣ��ɵã�![]() ���ɵó�����.
���ɵó�����.
��⣺������ɵã�M��NΪ�߶�BD�����ȷֵ㣬
��![]()
![]()
��ѡB.
�㾦��ƽ���ı���һ����ͶԱ��е������һ�����ȷ�ƽ���ı��ε�һ�Խ���.
�����͡���ѡ��
��������
10
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�A(2��0)��B(0��2)����M���߶�AB�ϣ���MO+MP��Сֵ��ƽ��Ϊs������P��x������ӵ�O�˶�����Aʱ(���P�ĺ�����Ϊx)��s����x�ĺ���ͼ�����Ϊ�� ��
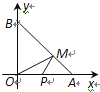
A.  B.
B. 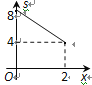 C.
C. 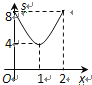 D.
D. 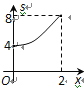
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�и�������Ϣ������������⣺
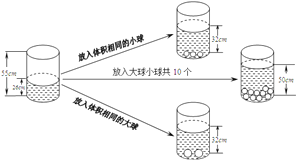
��1������һ��С��ˮ������ ��![]() ������һ������ˮ������
������һ������ˮ������ ![]() ��
��
��2�����Ҫʹˮ��������50![]() ��Ӧ�������С������ٸ���
��Ӧ�������С������ٸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C��ֱ��AB��DE֮���һ�㣬��ACD=90�㣬����������ʹ��AB��DE���ǣ�����
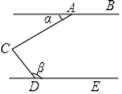
A. ����+����=180�� B. ����������=90�� C. ����=3���� D. ����+����=90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC����C=90����AC=12��BC=6��һ���߶�PQ=AB��P��Q����ֱ���AC����A�Ҵ�ֱ��AC������AX���˶���Ҫʹ��ABC����QPAȫ�ȣ���AP= ______ ��
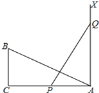
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����廧С������������ÿǧ��4Ԫ������ɽ����![]() ������ũó�г���ռ5��̯λ��ÿ��̯λ�������
������ũó�г���ռ5��̯λ��ÿ��̯λ�������![]() ����ÿ��̯λ���г�������Ϊÿ��20Ԫ���±�Ϊ����������ÿ������ۼ۸���ǰһ����ȼ۸���ǵ�������Ǽ�Ϊ��������Ϊ����.����һ�ļ۸���������ÿǧ��4Ԫ����۸����������1.3Ԫ.
����ÿ��̯λ���г�������Ϊÿ��20Ԫ���±�Ϊ����������ÿ������ۼ۸���ǰһ����ȼ۸���ǵ�������Ǽ�Ϊ��������Ϊ����.����һ�ļ۸���������ÿǧ��4Ԫ����۸����������1.3Ԫ.
���� | һ | �� | �� | �� | �� |
��ǰһ����ȼ۸���ǵ����/Ԫ | +1.3 | ��0.1 | +0.25 | +0.2 | ��0.5 |
����Ľ�����/ | 2500 | 2000 | 3000 | 1500 | 1000 |
��1������������۸�Ϊÿǧ�˶���Ԫ��
��2��С������������ÿǧ��4Ԫ������ɽ����![]() �����������г���ռ5��̯λ��С�������۹����в�������̯λ�����ķ��������ͳɱ����������棬�������ڱ��ܵ������й��˶���Ǯ�����������һ�㣿
�����������г���ռ5��̯λ��С�������۹����в�������̯λ�����ķ��������ͳɱ����������棬�������ڱ��ܵ������й��˶���Ǯ�����������һ�㣿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() ����
����![]() ��������ԭ��
��������ԭ��![]() ��������㣬���е�
��������㣬���е�![]() ��ԭ��
��ԭ��![]() ����࣬������
����࣬������![]() ��
��![]() .
.

��1����![]() ��
��![]() �������϶�Ӧ�����ֱ�Ϊ______��______.
�������϶�Ӧ�����ֱ�Ϊ______��______.
��2����![]() ��
��![]() ͬʱ�ֱ���ÿ��1����λ���Ⱥ�ÿ��2����λ���ȵ��ٶ������˶�.
ͬʱ�ֱ���ÿ��1����λ���Ⱥ�ÿ��2����λ���ȵ��ٶ������˶�.
�پ��������![]() ��
��
�ڵ�![]() ��
��![]() ���˶���ͬʱ����
���˶���ͬʱ����![]() ��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶������������
��ÿ��1����λ���ȵ��ٶȴ�ԭ�������˶������������![]() ��
��![]() ��
��![]() �е�ijһ���Ϊ�������������߶ε��е㣿
�е�ijһ���Ϊ�������������߶ε��е㣿
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com