
【题目】数轴上有![]() ,
,![]() ,
,![]() 三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“关联点”.例如数轴上点
三点,给出如下定义:若其中一个点与其它两个点的距离恰好满足2倍的数量关系,则称该点是其它两个点的“关联点”.例如数轴上点![]() ,
,![]() ,
,![]() 所表示的数分别为1, 3,4,此时点
所表示的数分别为1, 3,4,此时点![]() 是点
是点![]() ,
,![]() 的“关联点”.
的“关联点”.
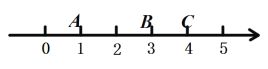
(1)若点![]() 表示数-2,点
表示数-2,点![]() 表示数1,下列各数-1, 2, 4, 6所对应的点分别是
表示数1,下列各数-1, 2, 4, 6所对应的点分别是![]() ,
,![]() ,
,![]() ,
,![]() ,其中是点
,其中是点![]() ,
,![]() 的“关联点”的是
的“关联点”的是
(2)点![]() 表示数-10,点
表示数-10,点![]() 表示数15,
表示数15,![]() 为数轴上一个动点:
为数轴上一个动点:
①若点![]() 在点
在点![]() 的左侧,且点
的左侧,且点![]() 是点
是点![]() ,
,![]() 的“关联点”,求此时点
的“关联点”,求此时点![]() 表示的数;
表示的数;
②若点![]() 在点
在点![]() 的右侧,点
的右侧,点![]() ,
,![]() ,
,![]() 中,有一个点恰好是其它两个点的“关联点”,请直接写出此时点
中,有一个点恰好是其它两个点的“关联点”,请直接写出此时点![]() 表示的数.
表示的数.
【答案】(1)C1或![]() ;(2)①-35或
;(2)①-35或![]() 或
或![]() ;②40、
;②40、![]() 、65.
、65.
【解析】
(1)根据题意由两个点的“关联点”的定义,求得CA与BC的关系,得到答案;
(2)①由题意设点P表示的数为x,根据PA,PB成2倍关系列方程求解;
②分当P为A、B关联点、A为P、B关联点、B为A、P关联点、B为P、A关联点四种可能列方程解答.
解:(1)C1A=1,C1B=2,C1B=2C1A,故C1符合题意;
C2A=4,C2B=1,故C2不符合题意;
C3A=6,C3B=3,C3A=2C3B,故C3符合题意;
C4A=8,C4B=5,故C4不符合题意.
故答案为:C1或![]() .
.
(2)①设点P表示的数为x,
当P点在点A左侧时,有PB=2PA,则 15-x=2(-10-x),解得 x=-35.所以点P表示的数为-35;
当P点在AB之间时,分别有PB=2PA和PA=2PB,列方程分别解得P点表示的数为![]() 和
和![]() ;
;
综上所述,当点P在点B的左侧时,点P表示的数为-35或![]() 或
或![]() .
.
②点![]() 在点
在点![]() 的右侧时,分三种情况:
的右侧时,分三种情况:
当P为A、B关联点时,设点P表示的数为x,
∵PA=2PB,
∴x+10=2(x-15),
解得x=40,
即此时点P表示的数40;
当B为A、P关联点时:设点P表示的数为x,
∵AB=2PB,
∴25=2(x-15),
解得x=![]() ,
,
即此时点P表示的数![]() ;
;
当B为P、A关联点时:设点P表示的数为x,
∵PB=2AB,
∴x-15=50,
解得x=65,
即此时点P表示的数65,
故答案为:40、![]() 、65.
、65.


科目:初中数学 来源: 题型:
【题目】定义:只有一组对角是直角的四边形叫做损矩形,连结它的两个非直角顶点的线段叫做这个损矩形的直径.
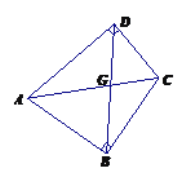
(1)如图,损矩形![]() 中,
中,![]() ,则该损矩形的直径是线段______.
,则该损矩形的直径是线段______.
(2)探究:在上述损矩形![]() 内,是否存在点
内,是否存在点![]() ,使
,使![]() 四个点都在以
四个点都在以![]() 为圆心的同一圆上,若存在,请指出点
为圆心的同一圆上,若存在,请指出点![]() 的具体位置___________________________;若不存在,请说明理由.
的具体位置___________________________;若不存在,请说明理由.
(3)实践:已知如图三条线段![]() ,求作相邻三边长顺次为
,求作相邻三边长顺次为![]() 的损矩形
的损矩形![]() (尺规作图,保留作图痕迹).
(尺规作图,保留作图痕迹).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如下图中的小正方形的大小相等,图1只有一个小正方形;图2是由4个小正方形构成的一个正方形;图3是由9个小正方形构成的一个正方形,…以此类推,每一个图形都是由小正方形构成的大正方形. 回答下列问题:
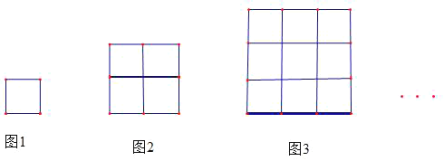
(1)图2比图1多________个小正方形,图3比图2多________个小正方形.
(2)图![]() 比图
比图![]() 多________个小正方形(用含
多________个小正方形(用含![]() 的式子表示)
的式子表示)
(3)猜想![]() ________.
________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知两直线![]() 与
与![]()
(1)在同一平面直角坐标系中作出两直线的图象;
(2)求出两直线的交点;
(3)根据图象指出x为何值时,![]() ;
;
(4)求这两条直线与x轴围成的三角形面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
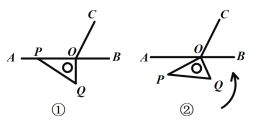
【题目】如图①,![]() 为直线
为直线![]() 上一点,作射线
上一点,作射线![]() ,使
,使![]() ,将一个直角三角尺如图摆放,直角顶点在点
,将一个直角三角尺如图摆放,直角顶点在点![]() 处,一条直角边
处,一条直角边![]() 在射线
在射线![]() 上. 将图
上. 将图![]() 中的三角尺绕点
中的三角尺绕点![]() 以每秒10°的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第
以每秒10°的速度按逆时针方向旋转(如图②所示),在旋转一周的过程中,第![]() 秒时,
秒时,![]() 所在直线恰好平分
所在直线恰好平分![]() ,则
,则![]() 的值为_________.
的值为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校初三(1)班50名学生需要参加体育“五选一”自选项目测试,班上学生所报自选项目的情况统计表如下:
自选项目 | 人数 | 频率 |
立定跳远 | 9 | 0.18 |
三级蛙跳 | 12 | a |
一分钟跳绳 | 8 | 0.16 |
投掷实心球 | b | 0.32 |
推铅球 | 5 | 0.10 |
合计 | 50 | 1 |
(1)求a,b的值;
(2)若将各自选项目的人数所占比例绘制成扇形统计图,求“一分钟跳绳”对应扇形的圆心角的度数;
(3)在选报“推铅球”的学生中,有3名男生,2名女生,为了了解学生的训练效果,从这5名学生中随机抽取两名学生进行推铅球测试,求所抽取的两名学生中至多有一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
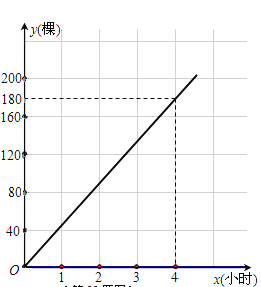
【题目】为了“绿化环境,美化家园”,3月12日(植树节)上午8点,某校901、902班同学同时参加义务植树.901班同学始终以同一速度种植树苗,种植树苗的棵数y1与种植时间x(小时)的函数图象如图所示;902班同学开始以1小时种植40棵的速度工作了1.5小时后,因需更换工具而停下休息半小时,更换工具后种植速度提高至原来的1.5倍.
(1)求902班同学上午11点时种植的树苗棵数;
(2)分别求出901班种植数量y1、902班种植数量y2与种植时间x(小时)之间的函数关系式,并在所给坐标系上画出y2关于x的函数图象;
(3)已知购买树苗不多于120棵时,每棵树苗的价格是20元;购买树苗超过120棵时,超过的部分每棵价格17元.若本次植树所购树苗的平均成本是18元,则两班同学上午几点可以共同完成本次植树任务?
【答案】(1)120棵;(2)见解析;(3)两班同学上午12点可以共同完成本次植树任务.
【解析】分析:![]() 直接进行计算即可.
直接进行计算即可.
![]() 用待定系数法求一次函数解析式即可, 902班的要分成3段.
用待定系数法求一次函数解析式即可, 902班的要分成3段.
![]() 当x=2时,两班同学共植树150棵,
当x=2时,两班同学共植树150棵,![]() 平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程
平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程![]() 求解即可.
求解即可.
详解:(1)902班同学上午11点时种植的树苗棵数为:
![]() (棵)
(棵)
(2)由图可知,y1是关于x的正比例函数,可设y1=k1x,经过(4,180),
代入可得![]()
∴![]() (x≥0),
(x≥0),
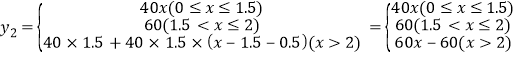 ,
,
y2关于x的函数图象如图所示.
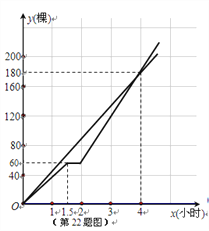
(3)当x=2时,两班同学共植树150棵,
![]() 平均成本:
平均成本:
所以,x>2,两班共植树(105x-60)棵.
![]() 由题意可得:
由题意可得:
解得:x=4.
![]() ,
,
所以,两班同学上午12点可以共同完成本次植树任务.
点睛:考查了待定系数法求一次函数解析式,一元一次方程的应用,注意分类讨论
的数学思想方法.
【题型】解答题
【结束】
23
【题目】在等腰直角△ABC中,,AC=BC,点P在斜边AB上(AP>BP).作AQ⊥AB,且AQ=BP,连结CQ(如图1).
(1)求证:△ACQ≌△BCP;
(2)延长QA至点R,使得∠RCP=45°,RC与AB交于点H,如图2.
①求证:CQ2=QA·QR ;
②判断三条线段AH、HP、PB的长度满足的数量关系,并说明理由.
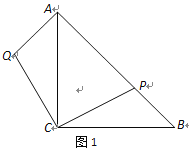
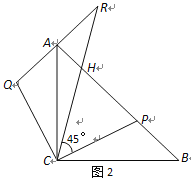
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是BC边的中点,
,点D是BC边的中点,![]() 于点E,
于点E,![]() 于点F.
于点F.

(1)![]() ________(用含α的式子表示)
________(用含α的式子表示)
(2)作射线DM与边AB交于点M,射线DM绕点D顺时针旋转![]() ,与AC边交于点N.根据条件补全图形,并写出DM与DN的数量关系,请说明理由.
,与AC边交于点N.根据条件补全图形,并写出DM与DN的数量关系,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com