
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

【答案】(1)经过2秒或4秒,△PBQ的面积等于8cm2;(2)线段PQ不能否将△ABC分成面积相等的两部分;(3)经过(5﹣![]() )秒,5秒,(5+
)秒,5秒,(5+![]() )秒后,△PBQ的面积为1.
)秒后,△PBQ的面积为1.
【解析】【试题分析】(1)设经过x秒,使△PBQ的面积等于8cm2,则PB=6-x,BQ=2x,列方程为: ![]() ,解得x1=2,x2=4,;(2)先计算△ABC的面积=
,解得x1=2,x2=4,;(2)先计算△ABC的面积=![]() ×6×8=24,
×6×8=24,
设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
![]() ,变形得,y2﹣6y+12=0,则△=b2﹣4ac=36﹣4×12=﹣12<0,即此方程无实数根,即线段PQ不能否将△ABC分成面积相等的两部分;
,变形得,y2﹣6y+12=0,则△=b2﹣4ac=36﹣4×12=﹣12<0,即此方程无实数根,即线段PQ不能否将△ABC分成面积相等的两部分;
(3)分类讨论,三种情况:
①点P在线段AB上,点Q在线段CB上(0<m<4),
设经过m秒,依题意列方程得: ![]()
m2﹣10m+23=0,
解得m1=5+![]() ,m2=5﹣
,m2=5﹣![]() ,
,
经检验,m1=5+![]() 不符合题意,舍去,
不符合题意,舍去,
∴m=5﹣![]() ;
;
②点P在线段AB上,点Q在射线CB上(4<n<6),
设经过n秒,依题意有
![]() ,
, ![]()
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(k>6),设经过k秒,依题意有
![]() (k﹣6)(2k﹣8)=1,k2﹣10k+23=0,
(k﹣6)(2k﹣8)=1,k2﹣10k+23=0,
解得k1=5+![]() ,k2=5﹣
,k2=5﹣![]() ,经检验,k1=5﹣
,经检验,k1=5﹣![]() 不符合题意,舍去,
不符合题意,舍去,
∴k=5+![]() ;综上所述,经过(5﹣
;综上所述,经过(5﹣![]() )秒,5秒,(5+
)秒,5秒,(5+![]() )秒后,△PBQ的面积为1.
)秒后,△PBQ的面积为1.
【试题解析】
(1)设经过x秒,使△PBQ的面积等于8cm2,依题意有
![]() (6﹣x)2x=8,
(6﹣x)2x=8,
解得x1=2,x2=4,
经检验,x1,x2均符合题意.
故经过2秒或4秒,△PBQ的面积等于8cm2;
(2)设经过y秒,线段PQ能否将△ABC分成面积相等的两部分,依题意有
△ABC的面积=![]() ×6×8=24,
×6×8=24,
![]() (6﹣y)2y=12,
(6﹣y)2y=12,
y2﹣6y+12=0,
∵△=b2﹣4ac=364×12=﹣12<0,
∴此方程无实数根,
∴线段PQ不能否将△ABC分成面积相等的两部分;
(3)①点P在线段AB上,点Q在线段CB上(0<x<4),
设经过m秒,依题意有
![]() (6﹣m)(8﹣2m)=1,
(6﹣m)(8﹣2m)=1,
m2﹣10m+23=0,
解得m1=5+![]() ,m2=5﹣
,m2=5﹣![]() ,
,
经检验,m1=5+![]() 不符合题意,舍去,
不符合题意,舍去,
∴m=5﹣![]() ;
;
②点P在线段AB上,点Q在射线CB上(4<x<6),
设经过n秒,依题意有
![]() (6﹣n)(2n﹣8)=1,
(6﹣n)(2n﹣8)=1,
m2﹣10n+25=0,
解得n1=n2=5,
经检验,n=5符合题意.
③点P在射线AB上,点Q在射线CB上(x>6),
设经过k秒,依题意有
![]() (k﹣6)(2k﹣8)=1,
(k﹣6)(2k﹣8)=1,
k2﹣10k+23=0,
解得k1=5+![]() ,k2=5﹣
,k2=5﹣![]() ,
,
经检验,k1=5﹣![]() 不符合题意,舍去,
不符合题意,舍去,
∴k=5+![]() ;
;
综上所述,经过(5﹣![]() )秒,5秒,(5+
)秒,5秒,(5+![]() )秒后,△PBQ的面积为1.
)秒后,△PBQ的面积为1.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,点C为线段AB上一点,△ACM,△CBN是等边三角形,直线AN,MC交于点E,直线BM,CN交于点F. 
(1)求证:AN=MB;
(2)求证:△CEF为等边三角形;
(3)将△ACM绕点C按逆时针方向旋转90°,其他条件不变,在(2)中画出符合要求的图形,并判断(1)(2)题中的两结论是否依然成立.并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘船由A港沿北偏东60°方向航行10km至B港,然后再沿北偏西30°方向航行10km至C港.
(1)求A,C两港之间的距离(结果保留到0.1km,参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732);
≈1.732);
(2)确定C港在A港的什么方向.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织教师为地震救灾捐款,分6个工会小组进行统计,其中第6工会小组尚未统计在内,如图:
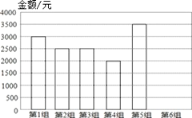
(1)求前5个工会小组捐款金额的众数、中位数和平均数;
(2)若全部6个小组的捐款平均数为2750元,求第6小组的捐款金额,并补全统计图.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在x轴的负半轴、y轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在y轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y= ![]() (x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,S矩形OABC=32,tan∠DOE= ![]() ,则BN的长为 .
,则BN的长为 . 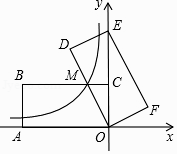
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=2,与x轴的一个交点坐标为(4,0),其部分图象如图所示,下列结论:
①抛物线过原点;
②4a+b+c=0;
③a﹣b+c<0;
④抛物线的顶点坐标为(2,b);
⑤当x<2时,y随x增大而增大.
其中结论正确的是( )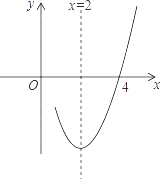
A.①②③
B.③④⑤
C.①②④
D.①④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.

理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂接受了20天内生产1200台GH型电子产品的总任务.已知每台GH型产品由4个G型装置和3个H型装置配套组成.工厂现有80名工人,每个工人每天能加工6个G型装置或3个H型装置.工厂将所有工人分成两组同时开始加工,每组分别加工一种装置,并要求每天加工的G、H型装置数量正好组成GH型产品.
(1)按照这样的生产方式,工厂每天能配套组成多少套GH型电子产品?
(2)工厂补充10名新工人,这些新工人只能独立进行G型装置的加工,且每人每天只能加工4个G型装置,则补充新工人后每天能配套生产多少产品?
(3)为了在规定期限内完成总任务,请问至少需要补充多少名(2)中的新工人才能在规定期内完成总任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com