
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
【答案】C
【解析】解:A、∵b2﹣4ac=(2m)2+12=4m2+12>0,
∴二次函数的图象与x轴有两个交点,故此选项正确,不合题意;
B、方程x2﹣2mx=3的两根之积为: ![]() =﹣3,故此选项正确,不合题意;
=﹣3,故此选项正确,不合题意;
C、m的值不能确定,故它的图象的对称轴位置无法确定,故此选项错误,符合题意;
D、∵a=1>0,对称轴x=m,
∴x<m时,y随x的增大而减小,故此选项正确,不合题意;
故答案为:C.
计算b2﹣4ac的值可对选项A作出判断;利用根与系数的关系,计算两根之积,可对选项B作出判断;根据a、b的符号确定对称轴的位置,但m的值不确定,可对选项C作出判断;根据二次函数的性质可对选项D作出判断,即可得出答案。


 一线名师权威作业本系列答案
一线名师权威作业本系列答案科目:初中数学 来源: 题型:
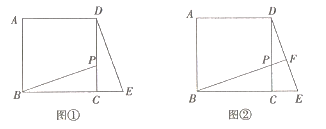
【题目】探究:如图①,在正方形ABCD中,点P在边CD上(不与点C、D重合),连接BP,将△BCP绕点C顺时针旋转至△DCE,点B的对应点是点D.旋转的角度是 度.应用:将图①中的BP延长交边DE于点F,其它条件不变,如图②,求∠BFE的度数。拓展:如图②,若DP=2CP,BC=6,则四边形ABED的面积是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
(1)有理化因式:两个含有根式的非零代数式相乘,如果它们的积不含有根式,那么这两个代数式相互叫做有理化因式.例如:![]() 的有理化因式是
的有理化因式是![]() ;
;![]() 的有理化因式是
的有理化因式是![]() .
.
(2)分母有理化:分母有理化又称“有理化分母”,也就是把分母中的根号化去.指的是如果代数式中分母有根号,那么通常将分子、分母同乘以分母的有理化因式,达到去分母中根号的目的.如:![]() ,
,![]()
问题解决:
(1)填空:![]() 的有理化因式是______.(x≥1)
的有理化因式是______.(x≥1)
(2)直接写出下列各式分母有理化的结果:
①![]() _____;②
_____;②![]() ______.
______.
(3)计算:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动.如果P,Q分别从A,B同时出发,线段PQ能否将△ABC分成面积相等的两部分?若能,求出运动时间;若不能说明理由.
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,问几秒后,△PBQ的面积为1?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家![]() 妈妈8:30从家出发,乘车沿相同路线去姥姥家
妈妈8:30从家出发,乘车沿相同路线去姥姥家![]() 在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是
在同一直角坐标系中,小亮和妈妈的行进路程与北京时间的函数图象如图所示,根据图象得到如下结论,其中错误的是![]()
![]()
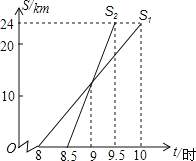
A. 9:00妈妈追上小亮B. 妈妈比小亮提前到达姥姥家
C. 小亮骑自行车的平均速度是![]() D. 妈妈在距家13km处追上小亮
D. 妈妈在距家13km处追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若两个一次函数与![]() 轴的交点关于
轴的交点关于![]() 轴对称,则称这两个一次函数为“对心函数”,这两个与
轴对称,则称这两个一次函数为“对心函数”,这两个与![]() 轴的交点为“对心点”.
轴的交点为“对心点”.

(1)写出一个![]() 的对心函数:________,这两个“对心点”为:_______;
的对心函数:________,这两个“对心点”为:_______;
(2)直线![]() 经过点
经过点![]() 和
和![]() ,直线
,直线![]() 的“对心函数”直线
的“对心函数”直线![]() 与
与![]() 轴的交点
轴的交点![]() 位于点
位于点![]() 的上方,且直线
的上方,且直线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 为直线
为直线![]() 的“对心点”.点
的“对心点”.点![]() 是动直线
是动直线![]() 上不与
上不与![]() 重合的一个动点,且
重合的一个动点,且![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图,直线![]() 与其“对心函数”直线
与其“对心函数”直线![]() 的交点
的交点![]() 位于第一象限,
位于第一象限,![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 的“对心点”,点
的“对心点”,点![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ;一动点
;一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() ,再沿线段
,再沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() 后停止,点
后停止,点![]() 在整个运动过程中所用最短时间为
在整个运动过程中所用最短时间为![]() 秒,求直线
秒,求直线![]() 的解析式.
的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:EF∥AD,∠1=∠2,∠BAC=75°.将求∠AGD的过程填写完整.
 解:∵EF∥AD (已知)
解:∵EF∥AD (已知)
∴∠2= ( )
又∵∠1=∠2 (已知)∴∠1=∠3( )
∴AB∥ ( )
∴∠BAC+ =180°( )
∵∠BAC=75°(已知)
∴∠AGD= .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com