
【题目】若两个一次函数与![]() 轴的交点关于
轴的交点关于![]() 轴对称,则称这两个一次函数为“对心函数”,这两个与
轴对称,则称这两个一次函数为“对心函数”,这两个与![]() 轴的交点为“对心点”.
轴的交点为“对心点”.

(1)写出一个![]() 的对心函数:________,这两个“对心点”为:_______;
的对心函数:________,这两个“对心点”为:_______;
(2)直线![]() 经过点
经过点![]() 和
和![]() ,直线
,直线![]() 的“对心函数”直线
的“对心函数”直线![]() 与
与![]() 轴的交点
轴的交点![]() 位于点
位于点![]() 的上方,且直线
的上方,且直线![]() 与直线
与直线![]() 交于点
交于点![]() ,点
,点![]() 为直线
为直线![]() 的“对心点”.点
的“对心点”.点![]() 是动直线
是动直线![]() 上不与
上不与![]() 重合的一个动点,且
重合的一个动点,且![]() ,试探究
,试探究![]() 与
与![]() 之间的数量关系,并说明理由.
之间的数量关系,并说明理由.
(3)如图,直线![]() 与其“对心函数”直线
与其“对心函数”直线![]() 的交点
的交点![]() 位于第一象限,
位于第一象限,![]() 、
、![]() 分别为直线
分别为直线![]() 、
、![]() 的“对心点”,点
的“对心点”,点![]() 为线段
为线段![]() 上一点(不含端点),连接
上一点(不含端点),连接![]() ;一动点
;一动点![]() 从
从![]() 出发,沿线段
出发,沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() ,再沿线段
,再沿线段![]() 以
以![]() 单位
单位![]() 秒的速度运动到点
秒的速度运动到点![]() 后停止,点
后停止,点![]() 在整个运动过程中所用最短时间为
在整个运动过程中所用最短时间为![]() 秒,求直线
秒,求直线![]() 的解析式.
的解析式.
【答案】(1)![]() (不唯一),
(不唯一),![]() ;
;![]() ;(2)详见解析;(3)
;(2)详见解析;(3)![]()
【解析】
(1)y=2x+6,令y=0,则x=-3,则这两个“对心点"为(-3,0)、(3,0),该对心函数只要过点(3,0)即可:
(2)根据![]() 可得
可得![]() ,
,![]()
则![]() 即可求解:
即可求解:
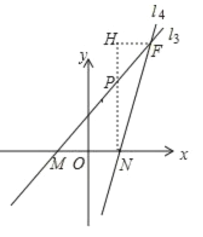
(3)过点F作x轴的平行线,过点N作y轴的平行线交l3于点P,两平行线交于点H,则此时t最小,即可求解.
(1)y=2x+6,令y=0,则x=-3
则这两个“对心点”为![]() 、
、![]() ;
;
对心点只要经过![]() 即可
即可
例如:y=-x+3,故答案不唯一
故答案为:y=-x+3(答案不唯一);(-3,0)、(3,0)
(2)![]()
设![]() ,
,![]()
则![]()
![]()
![]()

故答案为:![]()
(3)过点F作x轴的平行线,过点N作y轴的平行线l3于点P,两平行线交于点H,则此时t最小
直线l3:y=x+2,则直线的倾斜角为![]()
∴![]()
则PH=![]()
![]() =PN+PH=HN=6
=PN+PH=HN=6
故点F的纵坐标为6,则点F(4,6)
将M、F的坐标代入一次函数表达式y=kx+b
得![]()
解得![]()
![]()
故答案为:![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于二次函数y=x2﹣2mx﹣3,下列结论错误的是( )
A.它的图象与x轴有两个交点
B.方程x2﹣2mx=3的两根之积为﹣3
C.它的图象的对称轴在y轴的右侧
D.x<m时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请把以下证明过程补充完整:
已知:如图,∠A=∠F,∠C=∠D.点B,E分别在线段AC,DF上,对∠1=∠2进行说理.

理由:∵∠A=∠F(已知)
∴______∥FD (______)
∴∠D=______(两直线平行,内错角相等)
∵∠C=∠D(已知)
∴______=∠C(等量代换)
∴______∥______(同位角相等,两直线平行)
∴∠1=∠3(______)
∵∠2=∠3(______)
∴∠1=∠2(等量代换).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某企业用规格是170×40的标准板材作为原材料,按照如图1所示的裁法一或裁法二,裁剪出甲型与乙型两种板材(单位:cm)

(1)求图中a,b的值;
(2)若将50张标准板材按裁法一裁剪,10张标准板材按裁法二裁剪,裁剪后将得到的甲型与乙型板材做侧面或底面,做成如图2的竖式与横式两种无盖的装饰盒若干(接缝处的长度忽略不计).

①一共可裁剪出甲型板材______张,乙型板材______张;
②设可以做出竖式和横式两种无盖装饰盒一共x个,则x的最大值是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组![]() ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市一山区学校为部分家远的学生安排住宿,将部分教室改造成若干间住房. 如果每间住5人,那么有12人安排不下;如果每间住8人,那么有一间房还余一些床位,问该校可能有几间住房可以安排学生住宿?住宿的学生可能有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知边长为m的正方形面积为12,则下列关于m的说法中:①m2是有理数;②m的值满足m2﹣12=0;③m满足不等式组![]() ;④m是12的算术平方根. 正确有几个( )
;④m是12的算术平方根. 正确有几个( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com