
【题目】如图,点![]() 、点
、点![]() 是数轴上原点
是数轴上原点![]() 两侧的两点,其中点
两侧的两点,其中点![]() 在原点
在原点![]() 的左侧,且满足
的左侧,且满足![]() ,
,![]() .
.

(1)点![]() 、
、![]() 在数轴上对应的数分别为______和______.
在数轴上对应的数分别为______和______.
(2)点![]() 、
、![]() 同时分别以每秒1个单位长度和每秒2个单位长度的速度向左运动.
同时分别以每秒1个单位长度和每秒2个单位长度的速度向左运动.
①经过几秒后,![]() ;
;
②点![]() 、
、![]() 在运动的同时,点
在运动的同时,点![]() 以每秒1个单位长度的速度从原点向右运动,经过几秒后,点
以每秒1个单位长度的速度从原点向右运动,经过几秒后,点![]() 、
、![]() 、
、![]() 中的某一点成为其余两点所连线段的中点?
中的某一点成为其余两点所连线段的中点?
【答案】(1)-2和4;(2)①经过![]() 秒或
秒或![]() 秒,
秒,![]() ;②经过
;②经过![]() 秒或
秒或![]() 秒后,点
秒后,点![]() 、
、![]() 、
、![]() 中的某一点成为其余两点所连线段的中点.
中的某一点成为其余两点所连线段的中点.
【解析】
(1)设点A在数轴上对应的数为a,点B在数轴上对应的数为b.根据题意确定a、b的正负,得到关于a、b的方程,求解即可;
(2)①设t秒后OA=3OB.根据OA=3OB,列出关于t的一元一次方程,求解即可;
②根据中点的意义,得到关于t的方程,分三种情况讨论并求解:点P是AB的中点;点A是BP的中点;点B是AP的中点.
(1)设点A在数轴上对应的数为a,点B在数轴上对应的数为b,则OA=-a,OB=b
∵![]() ,
,
∴OA+OB=6
∴-a+b=6
∵![]() .
.
∴b=-2a
∴![]()
∴![]()
∴点A在数轴上对应的数为-2,点B在数轴上对应的数为4
故答案为:-2和4;
(2)①设![]() 秒后,
秒后,![]() ,则点A在数轴上对应的数为-2-t,点B在数轴上对应的数为4-2t,故OA=2+t
,则点A在数轴上对应的数为-2-t,点B在数轴上对应的数为4-2t,故OA=2+t
情况一:当点![]() 在点
在点![]() 右侧时,故OB=4-2t
右侧时,故OB=4-2t
∵![]()
则![]() ,
,
解得:![]() .
.
情况二:当点![]() 在点
在点![]() 左侧时,,故OB=2t-4
左侧时,,故OB=2t-4
∵![]()
则![]() ,
,
解得:![]() .
.
答:经过![]() 秒或
秒或![]() 秒,
秒,![]() .
.
②设经过![]() 秒后,点
秒后,点![]() 、
、![]() 、
、![]() 中的某一点成为其余两点所连线段的中点,此时点P在数轴上对应的数为t, 点A在数轴上对应的数为-2-t,点B在数轴上对应的数为4-2t
中的某一点成为其余两点所连线段的中点,此时点P在数轴上对应的数为t, 点A在数轴上对应的数为-2-t,点B在数轴上对应的数为4-2t
当点![]() 是
是![]() 的中点时,则
的中点时,则![]() ,
,
解得:![]() .
.
当点![]() 是
是![]() 的中点时,则
的中点时,则![]() .
.
解得:![]() .
.
当![]() 点是
点是![]() 的中点时,则
的中点时,则![]()
解得:![]() (不合题意,舍去)
(不合题意,舍去)
答:经过![]() 秒或
秒或![]() 秒后,点
秒后,点![]() 、
、![]() 、
、![]() 中的某一点成为其余两点所连线段的中点.
中的某一点成为其余两点所连线段的中点.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
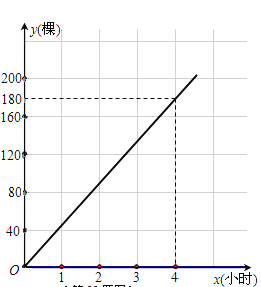
【题目】为了“绿化环境,美化家园”,3月12日(植树节)上午8点,某校901、902班同学同时参加义务植树.901班同学始终以同一速度种植树苗,种植树苗的棵数y1与种植时间x(小时)的函数图象如图所示;902班同学开始以1小时种植40棵的速度工作了1.5小时后,因需更换工具而停下休息半小时,更换工具后种植速度提高至原来的1.5倍.
(1)求902班同学上午11点时种植的树苗棵数;
(2)分别求出901班种植数量y1、902班种植数量y2与种植时间x(小时)之间的函数关系式,并在所给坐标系上画出y2关于x的函数图象;
(3)已知购买树苗不多于120棵时,每棵树苗的价格是20元;购买树苗超过120棵时,超过的部分每棵价格17元.若本次植树所购树苗的平均成本是18元,则两班同学上午几点可以共同完成本次植树任务?
【答案】(1)120棵;(2)见解析;(3)两班同学上午12点可以共同完成本次植树任务.
【解析】分析:![]() 直接进行计算即可.
直接进行计算即可.
![]() 用待定系数法求一次函数解析式即可, 902班的要分成3段.
用待定系数法求一次函数解析式即可, 902班的要分成3段.
![]() 当x=2时,两班同学共植树150棵,
当x=2时,两班同学共植树150棵,![]() 平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程
平均成本:不符合题意;,x>2,两班共植树(105x-60)棵.列出方程![]() 求解即可.
求解即可.
详解:(1)902班同学上午11点时种植的树苗棵数为:
![]() (棵)
(棵)
(2)由图可知,y1是关于x的正比例函数,可设y1=k1x,经过(4,180),
代入可得![]()
∴![]() (x≥0),
(x≥0),
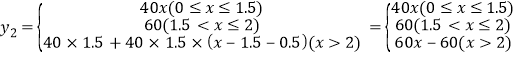 ,
,
y2关于x的函数图象如图所示.
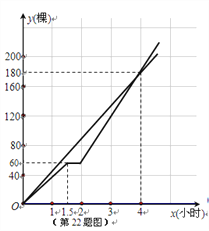
(3)当x=2时,两班同学共植树150棵,
![]() 平均成本:
平均成本:
所以,x>2,两班共植树(105x-60)棵.
![]() 由题意可得:
由题意可得:
解得:x=4.
![]() ,
,
所以,两班同学上午12点可以共同完成本次植树任务.
点睛:考查了待定系数法求一次函数解析式,一元一次方程的应用,注意分类讨论
的数学思想方法.
【题型】解答题
【结束】
23
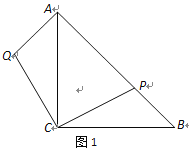
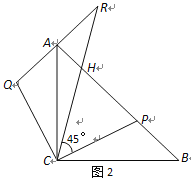
【题目】在等腰直角△ABC中,,AC=BC,点P在斜边AB上(AP>BP).作AQ⊥AB,且AQ=BP,连结CQ(如图1).
(1)求证:△ACQ≌△BCP;
(2)延长QA至点R,使得∠RCP=45°,RC与AB交于点H,如图2.
①求证:CQ2=QA·QR ;
②判断三条线段AH、HP、PB的长度满足的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D是BC边的中点,
,点D是BC边的中点,![]() 于点E,
于点E,![]() 于点F.
于点F.

(1)![]() ________(用含α的式子表示)
________(用含α的式子表示)
(2)作射线DM与边AB交于点M,射线DM绕点D顺时针旋转![]() ,与AC边交于点N.根据条件补全图形,并写出DM与DN的数量关系,请说明理由.
,与AC边交于点N.根据条件补全图形,并写出DM与DN的数量关系,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() ,直线
,直线![]() 分别与
分别与![]() 、
、![]() 交于点
交于点![]() 、
、![]() ,点
,点![]() 在直线
在直线![]() 上,
上,![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() .则下列结论:
.则下列结论:
①![]() 与
与![]() 是对顶角;②
是对顶角;②![]() ;
;
③![]() ;④
;④![]() .
.

其中正确结论的个数是( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,点
,点![]() 为平面内一点.
为平面内一点.
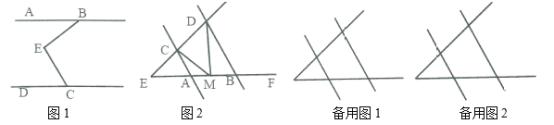
(1)如图1,![]() 和
和![]() 互余,小明说过
互余,小明说过![]() 作
作![]() ,很容易说明
,很容易说明![]() 。请帮小明写出具体过程;
。请帮小明写出具体过程;
(2)如图2,![]() ,当点
,当点![]() 在线段
在线段![]() 上移动时(点
上移动时(点![]() 与
与![]() ,
,![]() 两点不重合),指出
两点不重合),指出![]() 与
与![]() ,
,![]() 的数量关系?请说明理由;
的数量关系?请说明理由;
(3)在(2)的条件下,若点![]() 在
在![]() ,
,![]() 两点外侧运动(点
两点外侧运动(点![]() 与
与![]() ,
,![]() ,
,![]() 三点不重合)请直接写出
三点不重合)请直接写出![]() 与
与![]() ,
,![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
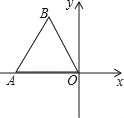
【题目】如图,点O为平面直角坐标系的原点,点A在x轴上,△OAB是边长为4的等边三角形,以O为旋转中心,将△OAB按顺时针方向旋转60°,得到△OA′B′,那么点A′的坐标为( )
A. (2,2![]() ) B. (﹣2,4) C. (﹣2,2
) B. (﹣2,4) C. (﹣2,2![]() ) D. (﹣2,2
) D. (﹣2,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点P的坐标是(a,b),从-2,-1,0,1,2这五个数中任取一个数作为a的值,再从余下的四个数中任取一个数作为b的值,则点P(a,b)在平面直角坐标系中第二象限内的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
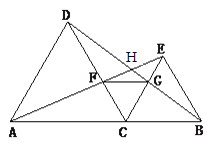
【题目】如图,C是线段AB上一点,分别以AC、CB为边作等边三角形ACD和CBE,连结AE、BD,AE交DC、DB分别为F点、H点,BD交CE于G点,连结FG.求证:① ∠FAC=∠HDC ;② ∠HFG=∠HAC;③ ∠BHA=120 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点A(10.0)及在第一象限的动点P(x,y),且x+y=12,设△OPA的面积为S。
(1)求S关于x的函数解析式;
(2)求x的取值范围;
(3)当S=15时,求P点坐标;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com