
ЁОЬтФПЁПШчЭМЃЌЪ§жсЩЯгаСНЖЈЕуAЁЂBЃЌЕу![]() БэЪОЕФЪ§ЮЊ6ЃЌЕуBдкЕуAЕФзѓВрЃЌЧвAB=20ЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈt>0ЃЉ.
БэЪОЕФЪ§ЮЊ6ЃЌЕуBдкЕуAЕФзѓВрЃЌЧвAB=20ЃЌЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌЩшдЫЖЏЪБМфЮЊtУыЃЈt>0ЃЉ.
![]()
ЃЈ1ЃЉаДГіЪ§жсЩЯЕуBБэЪОЕФЪ§______ЃЌЕуPБэЪОЕФЪ§гУКЌtЕФЪНзгБэЪОЃК_______ЃЛ
ЃЈ2ЃЉЩшЕуMЪЧAPЕФжаЕуЃЌЕуNЪЧPBЕФжаЕу.ЕуPдкжБЯпABЩЯдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮMNЕФГЄЖШЪЧЗёЛсЗЂЩњБфЛЏЃПШєЗЂЩњБфЛЏЃЌЧыЫЕУїРэгЩЃЛШєВЛБфЛЏЃЌЧѓГіЯпЖЮMNЕФГЄЖШ.
ЃЈ3ЃЉЖЏЕуRДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌШєЕуPЁЂRЭЌЪБГіЗЂЃЛЕБЕуPдЫЖЏЖрЩйУыЪБЃПгыЕуRЕФОрРыЮЊ2ИіЕЅЮЛГЄЖШ.
ЁОД№АИЁПЃЈ1ЃЉ-14ЃЌ6-4tЃЛЃЈ2ЃЉЯпЖЮMNЕФГЄЖШВЛЗЂЩњБфЛЏЃЌMNЕФГЄЖШЮЊ10cmЃЛЃЈ3ЃЉЕуPдЫЖЏ11УыЛђ9УыЪБЃЌгыЕуRЕФОрРыЮЊ2ИіЕЅЮЛГЄЖШ.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕуBдкЕуAЕФзѓВрМАЪ§жсЩЯСНЕуМфОрРыЙЋЪНМДПЩЕУГіЕуBБэЪОЕФЪ§ЃЌРћгУОрРы=ЫйЖШЁСЪБМфПЩБэЪОAPЕФОрРыЃЌМДПЩБэЪОГіЕуPБэЪОЕФЪ§ЃЛ
ЃЈ2ЃЉИљОнжаЕуЕФЖЈвхПЩЧѓГіAMЁЂBNЕФГЄЃЌИљОнMN=AB-BN-AMМДПЩЧѓГіMNЕФГЄЃЌМДПЩЕУД№АИЃЛ
ЃЈ3ЃЉРћгУОрРы=ЫйЖШЁСЪБМфПЩЕУГіЕуRКЭЕуPБэЪОЕФЪ§ЃЌИљОнЪ§жсЩЯСНЕуМфОрРыЙЋЪНСаЗНГЬЧѓГіtжЕМДПЩ.
ЃЈ1ЃЉЁпЕу![]() БэЪОЕФЪ§ЮЊ6ЃЌЕуBдкЕуAЕФзѓВрЃЌЧвAB=20ЃЌ
БэЪОЕФЪ§ЮЊ6ЃЌЕуBдкЕуAЕФзѓВрЃЌЧвAB=20ЃЌ
ЁрЕуBБэЪОЕФЪ§ЮЊ6-20=-14ЃЌ
ЁпЖЏЕуPДгЕуAГіЗЂЃЌвдУПУы4ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌ
ЁрЕуPБэЪОЕФЪ§ЮЊ6-4tЃЌ
ЙЪД№АИЮЊЃК-14ЃЌ6-4t
ЃЈ2ЃЉШчЭМЃЌЁпЕуMЪЧAPЕФжаЕуЃЌЕуPЕФЫйЖШЮЊУПУы4ИіЕЅЮЛГЄЖШЃЌ
ЁрAM=![]() ЁС4t=2tЃЌ
ЁС4t=2tЃЌ
ЁпЕуNЪЧPBЕФжаЕуЃЌ
ЁрBN=![]() ЁС(20-4t)=10-2tЃЌ
ЁС(20-4t)=10-2tЃЌ
ЁрMN=AB-BN-AM=20-(10-2t)-2t=10ЃЌ
![]()
ЁрЕуPдкжБЯпABЩЯдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮMNЕФГЄЖШВЛЗЂЩњБфЛЏЃЌMNЕФГЄЖШЮЊ10cm.
ЃЈ3ЃЉЁпЖЏЕуRДгЕуBГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЪ§жсЯђзѓдШЫйдЫЖЏЃЌ
ЁрЕуRБэЪОЕФЪ§ЪЧ-14-2tЃЌ
ЁпЕуPБэЪОЕФЪ§ЮЊ6-4tЃЌЕуPгыЕуRЕФОрРыЮЊ2ИіЕЅЮЛГЄЖШ.
ЁрPR=![]() =2ЃЌМД
=2ЃЌМД![]() =2ЃЌ
=2ЃЌ
НтЕУЃКt=11Лђt=9ЃЌ
ЁрЕуPдЫЖЏ11УыЛђ9УыЪБЃЌгыЕуRЕФОрРыЮЊ2ИіЕЅЮЛГЄЖШ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊЕу![]() дкЭЌвЛЬѕжБЯпЩЯЃЌ
дкЭЌвЛЬѕжБЯпЩЯЃЌ![]() ЦНЗж
ЦНЗж![]() .
.
ЃЈ1ЃЉЬюПеЃКгы![]() ЛЅгрЕФНЧга ЃЛ
ЛЅгрЕФНЧга ЃЛ
ЃЈ2ЃЉШє![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФЖШЪ§ЃЛ
ЕФЖШЪ§ЃЛ
ЃЈ3ЃЉЧѓжЄЃК![]() ЪЧ
ЪЧ![]() ЕФЦНЗжЯп.
ЕФЦНЗжЯп.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИљОнЭМжаИјГіЕФаХЯЂЃЌНтД№ЯТСаЮЪЬтЃК
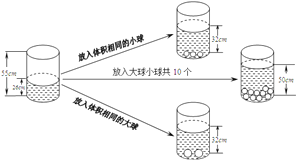
ЃЈ1ЃЉЗХШывЛИіаЁЧђЫЎУцЩ§Ип ЃЌ![]() ЃЌЗХШывЛИіДѓЧђЫЎУцЩ§Ип
ЃЌЗХШывЛИіДѓЧђЫЎУцЩ§Ип ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЙћвЊЪЙЫЎУцЩЯЩ§ЕН50![]() ЃЌгІЗХШыДѓЧђЁЂаЁЧђИїЖрЩйИіЃП
ЃЌгІЗХШыДѓЧђЁЂаЁЧђИїЖрЩйИіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
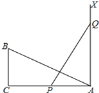
ЁОЬтФПЁПШчЭМЃЌдкRtЁїABCЃЌЁЯC=90ЁуЃЌAC=12ЃЌBC=6ЃЌвЛЬѕЯпЖЮPQ=ABЃЌPЁЂQСНЕуЗжБ№дкACКЭЙ§ЕуAЧвДЙжБгкACЕФЩфЯпAXЩЯдЫЖЏЃЌвЊЪЙЁїABCКЭЁїQPAШЋЕШЃЌдђAP= ______ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАЫ(2)АрзщжЏСЫвЛДЮОЕфЫаЖСБШШќЃЌМзЁЂввСНЖгИї10ШЫЕФБШШќГЩМЈШчЯТБэ(10ЗжжЦ)ЃК
Мз | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
вв | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)МзЖгГЩМЈЕФжаЮЛЪ§ЪЧ ЗжЃЌввЖгГЩМЈЕФжкЪ§ЪЧ ЗжЃЛ
(2)МЦЫуввЖгЕФЦНОљГЩМЈКЭЗНВюЃЛ
(3)вбжЊМзЖгГЩМЈЕФЗНВюЪЧ1.4ЃЌдђГЩМЈНЯЮЊећЦыЕФЪЧ ЖгЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИіЬхЛЇаЁЭѕдкЩЯжмШевдУПЧЇПЫ4дЊТђНјН№З№ЩНЯЪЫё![]() ЃЌНјШыХЉУГЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌУПИіЬЏЮЛзюЖрШнФЩ
ЃЌНјШыХЉУГЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌУПИіЬЏЮЛзюЖрШнФЩ![]() ЯЪЫёЃЌУПИіЬЏЮЛЕФЪаГЁЙмРэМлЮЊУПЬь20дЊЃЌЯТБэЮЊБОжмФкЯЪЫёУПЬьЕФЯњЪлМлИёгыЧАвЛЬьЯрБШМлИёЕФеЧЕјЧщПіЃЈеЧМЧЮЊе§ЃЌЕјМЧЮЊИКЃЉ.аЧЦквЛЕФМлИёЪЧдкжмШеУПЧЇПЫ4дЊТђНјМлИёЛљДЁЩЯеЧСЫ1.3дЊ.
ЯЪЫёЃЌУПИіЬЏЮЛЕФЪаГЁЙмРэМлЮЊУПЬь20дЊЃЌЯТБэЮЊБОжмФкЯЪЫёУПЬьЕФЯњЪлМлИёгыЧАвЛЬьЯрБШМлИёЕФеЧЕјЧщПіЃЈеЧМЧЮЊе§ЃЌЕјМЧЮЊИКЃЉ.аЧЦквЛЕФМлИёЪЧдкжмШеУПЧЇПЫ4дЊТђНјМлИёЛљДЁЩЯеЧСЫ1.3дЊ.
аЧЦк | вЛ | Жў | Ш§ | ЫФ | Юх |
гыЧАвЛЬьЯрБШМлИёЕФеЧЕјЧщПі/дЊ | +1.3 | Ѓ0.1 | +0.25 | +0.2 | Ѓ0.5 |
ЕБЬьЕФНЛвзСП/ | 2500 | 2000 | 3000 | 1500 | 1000 |
ЃЈ1ЃЉЯЪЫёЯњЪлзюИпМлИёЮЊУПЧЇПЫЖрЩйдЊЃП
ЃЈ2ЃЉаЁЭѕдкЩЯжмШевдУПЧЇПЫ4дЊТђНјН№З№ЩННтЫё![]() ЃЌНјШыХњЗЂЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌаЁЭѕдкЯњЪлЙ§ГЬжаВЩгУж№ВНМѕЩйЬЏЮЛИіЪ§ЕФЗНЗЈРДНЕЕЭГЩБОЃЌдіМгЪевцЃЌетбљЫћдкБОжмЕФТђТєжаЙВзЌСЫЖрЩйЧЎЃПЧыФуАяЫћЫувЛЫуЃП
ЃЌНјШыХњЗЂЪаГЁКѓЙВеМ5ИіЬЏЮЛЃЌаЁЭѕдкЯњЪлЙ§ГЬжаВЩгУж№ВНМѕЩйЬЏЮЛИіЪ§ЕФЗНЗЈРДНЕЕЭГЩБОЃЌдіМгЪевцЃЌетбљЫћдкБОжмЕФТђТєжаЙВзЌСЫЖрЩйЧЎЃПЧыФуАяЫћЫувЛЫуЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЭѕДѓВЎМЦЛЎдкздМвЕФгуЬСРяЭЖЗХЦеЭЈгуУчКЭКьЩЋгуУчЃЌашвЊЙКТђетСНжжгуУч2000ЮВЃЌЙКТђетСНжжгуУчЕФЯрЙиаХЯЂШчЯТБэЃК
ЦЗжжЯюФП | ЕЅМлЃЈдЊ/ЮВЃЉ | бјжГЗбгУЃЈдЊ/ЮВЃЉ |
ЦеЭЈгуУч | 0.5 | 1 |
КьЩЋгуУч | 1 | 1 |
ЩшЙКТђЦеЭЈгуУчxЮВЃЌбјжГетаЉгуУчЕФзмЗбгУЮЊyдЊ.
ЃЈ1ЃЉаДГіyЃЈдЊЃЉгыxЃЈЮВЃЉжЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉШчЙћЙКТђУПжжгуУчВЛЩйгк600ЮВЃЌдкзмгуУч2000ЮВВЛБфЕФЬѕМўЯТЃЌбјжГетаЉгуУчЕФзюЕЭЗбгУЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЙигкxЕФвЛдЊЖўДЮЗНГЬ![]() гаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИіИљЮЊСэвЛИіИљЕФ2БЖЃЌдђГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЎвдЯТЙигкБЖИљЗНГЬЕФЫЕЗЈЃЌе§ШЗЕФЪЧ________ЃЎЃЈаДГіЫљгае§ШЗЫЕЗЈЕФађКХЃЉЃЎ
гаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИіИљЮЊСэвЛИіИљЕФ2БЖЃЌдђГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЎвдЯТЙигкБЖИљЗНГЬЕФЫЕЗЈЃЌе§ШЗЕФЪЧ________ЃЎЃЈаДГіЫљгае§ШЗЫЕЗЈЕФађКХЃЉЃЎ
ЂйЗНГЬ![]() ЪЧБЖИљЗНГЬЃЛ
ЪЧБЖИљЗНГЬЃЛ
ЂкШє![]() ЪЧБЖИљЗНГЬЃЌдђ
ЪЧБЖИљЗНГЬЃЌдђ![]() ЃЛ
ЃЛ
ЂлШєЕу![]() дкЗДБШР§КЏЪ§
дкЗДБШР§КЏЪ§![]() ЕФЭМЯёЩЯЃЌдђЙигк
ЕФЭМЯёЩЯЃЌдђЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() ЪЧБЖИљЗНГЬЃЛ
ЪЧБЖИљЗНГЬЃЛ
ЂмШєЗНГЬ![]() ЪЧБЖИљЗНГЬЃЌЧвЯрвьСНЕу
ЪЧБЖИљЗНГЬЃЌЧвЯрвьСНЕу![]() ЃЌ
ЃЌ ![]() ЖМдкХзЮяЯп
ЖМдкХзЮяЯп![]() ЩЯЃЌдђЗНГЬ
ЩЯЃЌдђЗНГЬ![]() ЕФвЛИіИљЮЊ
ЕФвЛИіИљЮЊ![]() ЃЎ
ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЯпЖЮAB=12ЃЌЖЏЕуPДгAГіЗЂЃЌвдУПУы2ИіЕЅЮЛЕФЫйЖШбиЩфЯпABдЫЖЏЃЌMЮЊAPЕФжаЕуЃЎ
ЃЈ1ЃЉГіЗЂЖрЩйУыКѓЃЌPB=2AMЃП
ЃЈ2ЃЉЕБPдкЯпЖЮABЩЯдЫЖЏЪБЃЌЪдЫЕУї2BMЉBPЮЊЖЈжЕЃЎ
ЃЈ3ЃЉЕБPдкABбгГЄЯпЩЯдЫЖЏЪБЃЌNЮЊBPЕФжаЕуЃЌЯТСаСНИіНсТлЃКЂйMNГЄЖШВЛБфЃЛЂкMA+PNЕФжЕВЛБфЃЌбЁдёвЛИіе§ШЗЕФНсТлЃЌВЂЧѓГіЦфжЕЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com