
����Ŀ��С��ÿ������7��30�Ӽҳ����������![]() ��ѧУ��ѧ��һ�죬С����
��ѧУ��ѧ��һ�죬С����![]() ���ٶ���ѧ��
���ٶ���ѧ��![]() ��С���ְַ������������������飬�ְ���������������ȥ��С��.
��С���ְַ������������������飬�ְ���������������ȥ��С��.
��1������ְ���![]() ���ٶ�С�����ְ���С��ʱ����ѧУ��Զ��
���ٶ�С�����ְ���С��ʱ����ѧУ��Զ��
��2������ְָպ�����ѧУ�ſ���С�����ְֵ��ٶ��Ƕ��٣�
��3���ְ���![]() ���ٶ���С�����������С����ʱԭ·ԭ�ٷ��أ����鵢���ʱ����Բ��ƣ������ؼҵ�ʱ���Ƕ��٣�
���ٶ���С�����������С����ʱԭ·ԭ�ٷ��أ����鵢���ʱ����Բ��ƣ������ؼҵ�ʱ���Ƕ��٣�
���𰸡���1���ְ���С��ʱ����ѧУ200�ף���2���ְֵ��ٶ���![]() ����3���ְַ��ؼҵ�ʱ����7��43.
����3���ְַ��ؼҵ�ʱ����7��43.
��������
��1����ְ�t���Ӻ���С�������ݴ�ʱС����ʻ��·��=�ְ���ʻ��·�̣��з��̲��ⷽ�̣�Ȼ������ְ���С��ʱ����ѧУ�ж�Զ��
��2�������С���Ӽҵ�ѧУ��ʱ�䣬Ȼ������ְִӼҵ�ѧУ��ʱ�䣬��������ְֵ��ٶȣ�
��3����ְ�x���Ӻ���С��, ���ݴ�ʱС����ʻ��·��=�ְ���ʻ��·�̣��з��̲��ⷽ�̣����ݰְ�ԭ�ٷ��ؼ����������ʱ��ʱ�䣬�Ӷ�����ְַ��ؼҵ�ʱ��.
�⣺��1����ְ�t���Ӻ���С��
�������֪��80��t��5��=160t
��ã�t=5
��ְ���С��ʱ����ѧУ1000��160��5=200���ף�
�𣺰ְ���С��ʱ����ѧУ200�ף�
��2��С���Ӽҵ�ѧУ����ʱ��Ϊ��1000��80=12.5�����ӣ�
��ְִӼҵ�ѧУ����ʱ��Ϊ��12.5��5=7.5�����ӣ�
��ְֵ��ٶ�Ϊ��1000��7.5=![]()
�𣺰ְֵ��ٶ���![]() ��
��
��3����ְ�x���Ӻ���С��
�������֪��80��x��5��=180x
��ã�x=4
�ְ߰�ԭ�ٷ���
���Ҳ����4����
��ʱ��ʱ��Ϊ��7��30��0:05��0:04��0:04=7��43
�𣺰ְַ��ؼҵ�ʱ����7��43.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2011���ݰ�˳��10��3�֣�һֻ�����ڵ�һ����x�ᡢy�����������ڵ�һ���ӣ�����ԭ��������(0��1)��Ȼ����Ű�ͼ�м�ͷ��ʾ��������[��(0��0)��(0��1) ��(1��1) ����1��0������]����ÿ������һ����λ����ô��35��ʱ��������λ�õ������ǣ� ��

A. (4��O) B. (5��0) C. (0��5) D. (5��5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��D��BC��һ�㣬DE��AB����AC�ڵ�E��DF��AC����AB��F��

��1��ֱ��д��ͼ�����BAC���ɵ�ͬ���ڽǣ�
��2����˵����A���EDF��ȵ����ɣ�
��3������BDE +��CDF��234�㣬���BAC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
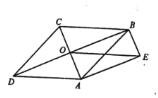
����Ŀ����ͼ��ƽ���ı���ABCD�ĶԽ���AC, BD�ཻ�ڵ�O����AE��BD, BE��AC, OE= CD.
��1����֤���ı���ABCD�����Σ�
��2����AD=2,���ı���ABCD����״��__________ʱ���ı���AOBE�����ȡ�����ֵ��__________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
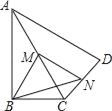
����Ŀ����ͼ�����ı���ABCD�У���ABC=90�㣬AC=AD��M��N�ֱ�ΪAC��CD���е㣬����BM��MN��BN����BAD=60�㣬ACƽ�֡�BAD��AC=2��BN�ij�Ϊ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
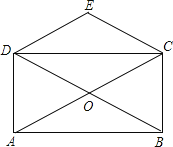
����Ŀ����ͼ������ABCD�ĶԽ���AC��BD���ڵ�O��CE��BD��DE��AC��
��1��֤�����ı���OCEDΪ���Σ�
��2����AC=4�����ı���CODE���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������y=ax2+bx+3��a��0��������A����1��0����B��![]() ��0��������y���ཻ�ڵ�C��
��0��������y���ཻ�ڵ�C��
��1�������������ߵı���ʽ��
��2�����ACB�Ķ�����
��3�����D�����������ߵ�һ������һ�㣬���ڶԳ�����Ҳ࣬��E���߶�AC�ϣ���DE��AC������DCE���AOC����ʱ�����D�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺ֻ��һ��Խ���ֱ�ǵ��ı��ν�������Σ���������������ֱ�Ƕ�����߶ν����������ε�ֱ����
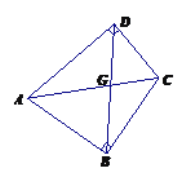
��1����ͼ�������![]() �У�
�У�![]() ���������ε�ֱ�����߶�______��
���������ε�ֱ�����߶�______��
��2��̽���������������![]() �ڣ��Ƿ���ڵ�
�ڣ��Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �ĸ��㶼����
�ĸ��㶼����![]() ΪԲ�ĵ�ͬһԲ�ϣ������ڣ���ָ����
ΪԲ�ĵ�ͬһԲ�ϣ������ڣ���ָ����![]() �ľ���λ��___________________________���������ڣ���˵������.
�ľ���λ��___________________________���������ڣ���˵������.
��3��ʵ������֪��ͼ�����߶�![]() �������������߳�˳��Ϊ
�������������߳�˳��Ϊ![]() �������
�������![]() ���߹���ͼ��������ͼ�ۼ�����
���߹���ͼ��������ͼ�ۼ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�е�С�����εĴ�С��ȣ�ͼ1ֻ��һ��С�����Σ�ͼ2����4��С�����ι��ɵ�һ�������Σ�ͼ3����9��С�����ι��ɵ�һ�������Σ����Դ����ƣ�ÿһ��ͼ�ζ�����С�����ι��ɵĴ�������. �ش��������⣺
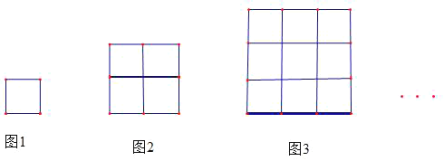
��1��ͼ2��ͼ1��________��С�����Σ�ͼ3��ͼ2��________��С������.
��2��ͼ![]() ��ͼ
��ͼ![]() ��________��С�����Σ��ú�
��________��С�����Σ��ú�![]() ��ʽ�ӱ�ʾ��
��ʽ�ӱ�ʾ��
��3������![]() ________.
________.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com