Question

3．在等腰三角形ABC中，当顶角BAC等于多少度时，△ABC能够被过一个顶点的一条直线分割成2个较小的等腰三角形？请画出符合条件的△ABC的示意图，并写出△ABC各内角的度数．

Answer 1

分析 因为题中没有指明这个等腰三角形是什么形状，故应该分四种情况进行分析，从而得到答案．

解答 解：（1）如图，△ABC中，AB=AC，BD=AD，AC=CD时，
∵AB=AC，BD=AD，AC=CD，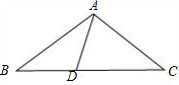
∴∠B=∠C=∠BAD，∠CDA=∠CAD，
∵∠CDA=2∠B，
∴∠CAB=3∠B，
∵∠BAC+∠B+∠C=180°，
∴5∠B=180°，
∴∠B=36°，
∴∠BAC=108°．
故△ABC各内角的度数分别为108°、36°、36°．
（2）如图，△ABC中，AB=AC，AD=BD=CD时，
∵AB=AC，AD=BD=CD，
∴∠B=∠C=∠DAC=∠DAB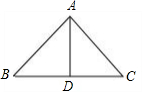
∴∠BAC=2∠B
∵∠BAC+∠B+∠C=180°，
∴4∠B=180°，
∴∠B=45°，
∴∠BAC=90°．
故△ABC各内角的度数分别为90°、45°、45°
（3）如图，△ABC中，AB=AC，BD=AD=BC时，
∵AB=AC，BD=AD=BC，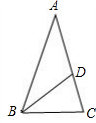
∴∠B=∠C，∠A=∠ABD，∠BDC=∠C
∵∠BDC=2∠A，
∴∠C=2∠A=∠B，
∵∠A+∠ABC+∠C=180°，
∴5∠A=180°，
∴∠A=36°．
故△ABC各内角的度数分别为36°、72°、72°
（4）如图，△ABC中，AB=AC，BD=AD，CD=BC时，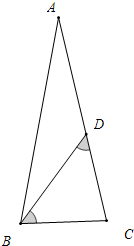
假设∠A=x，AD=BD，
∴∠DBA=x，
∵AB=AC，
∴∠C=$\frac{180-x}{2}$，
∵CD=BC，
∴∠BDC=∠DBC，
∴2x=$\frac{180-x}{2}$-x，解得x=$\frac{180°}{7}$．
∴∠A=$\frac{180°}{7}$．
故△ABC各内角的度数分别为$\frac{180°}{7}$、$\frac{540°}{7}$、$\frac{540°}{7}$．

点评 本题考查等腰三角形的性质、三角形外角的性质以及三角形内角和定理等知识，灵活运用这些知识解题是解题的关键．