
分析 作OE⊥AB于E,OF⊥CD于F,连OA,OC,由垂径定理得AE=$\frac{1}{2}$AB=5,CF=$\frac{1}{2}$CD=12,由于AB∥CD,易得E、O、F三点共线,在Rt△AOE和Rt△OCF中,利用勾股定理分别计算出OE与OF,然后讨论:当圆心O在弦AB与CD之间时,AB与CD的距离=OE+OF;当圆心O在弦A′B′与CD的外部时,AB与CD的距离=OE-OF.
解答 解:如图作OE⊥AB于E,OF⊥CD于F,连OA,OC,OA=OC=13,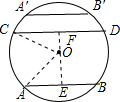
则AE=$\frac{1}{2}$AB=5,CF=$\frac{1}{2}$CD=12,
∵AB∥CD,
∴E、O、F三点共线,
在Rt△COF中,OF=$\sqrt{O{C}^{2}-C{F}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
在Rt△AOE中,OE=$\sqrt{O{A}^{2}-A{E}^{2}}$=$\sqrt{1{3}^{2}-{5}^{2}}$=12,
当圆心O在弦AB与CD之间时,AB与CD的距离=OE+OF=12+5=17;
当圆心O在弦A′B′与CD的外部时,AB与CD的距离=OE-OF=12-5=7.
所以AB与CD的距离是17或7.
点评 本题考查了垂径定理:垂直于弦的直径平分弦,并且平分弦所对的弧.也考查了勾股定理以及分类讨论思想的运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
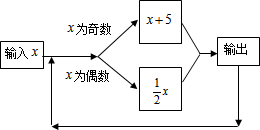 按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,请你探索第2015次得到的结果为4.
按如图所示的程序计算,若开始输入的x的值为24,我们发现第一次得到的结果为12,第2次得到的结果为6,…,请你探索第2015次得到的结果为4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
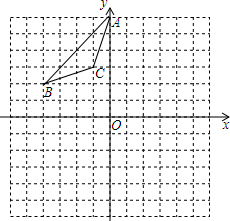 如图,△ABC的三个顶点的坐标分别为A(0,6),B(-4,2),C(-1,3).
如图,△ABC的三个顶点的坐标分别为A(0,6),B(-4,2),C(-1,3).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
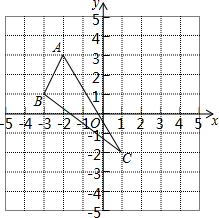 在平面直角坐标系中,△ABC的三个顶点的位置如图所示.
在平面直角坐标系中,△ABC的三个顶点的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查奥运会100米决赛参赛运动员兴奋剂的使用情况 | |
| B. | 调查一个班级的学生对“中国好声音”节目的知晓率 | |
| C. | 调查金牛区中小学生每天课外体育锻炼的时间 | |
| D. | 调查“玉兔号”飞船各零部件的质量情况 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com