
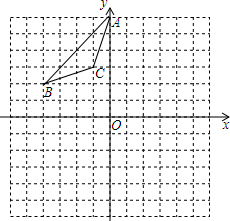
 如图,△ABC的三个顶点的坐标分别为A(0,6),B(-4,2),C(-1,3).
如图,△ABC的三个顶点的坐标分别为A(0,6),B(-4,2),C(-1,3).分析 (1)作出各点关于y轴的对称点,再顺次连接即可;
(2)作点C关于x轴的对称点C′,连接B1C′交x轴于点P,则点P即为所求点.
解答 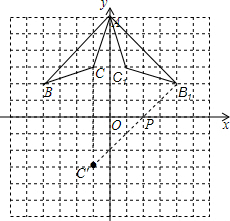 解:(1)如图,△AB1C1即为所求;
解:(1)如图,△AB1C1即为所求;
(2)∵C(-1,3),
∴C′(-1,-3).
设直线B1C′的解析式为y=kx+b(k≠0),
∵B1(4,2),
∴$\left\{\begin{array}{l}-3=-k+b\\ 2=4k+b\end{array}\right.$,解得$\left\{\begin{array}{l}k=1\\ b=-2\end{array}\right.$,
∴直线B1C′的解析式为y=x-2,
∴当y=0时,x=2,
∴P(2,0).
点评 本题考查的是作图-轴对称变换,熟知关于y轴对称的点的坐标特点是解答此题的关键.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:初中数学 来源: 题型:选择题
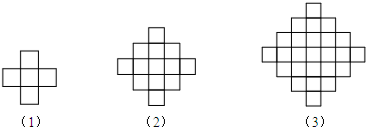
| A. | 181 | B. | 145 | C. | 100 | D. | 88 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com