
【题目】如图,抛物线![]() (a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,过点A的直线y=﹣x+4交抛物线于点C.
(1)求此抛物线的解析式;
(2)在直线AC上有一动点E,当点E在某个位置时,使△BDE的周长最小,求此时E点坐标;
(3)当动点E在直线AC与抛物线围成的封闭线A→C→B→D→A上运动时,是否存在使△BDE为直角三角形的情况,若存在,请直接写出符合要求的E点的坐标;若不存在,请说明理由.

【答案】(1)![]() ;(2)E(
;(2)E(![]() ,
,![]() );(3)E(3,1)或(
);(3)E(3,1)或(![]() ,
,![]() ).
).
【解析】(1)∵抛物线![]() (a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,∴
(a≠0)与x轴交于A(4,0)、B(﹣1,0)两点,∴![]() ,∴
,∴![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)如图1,作点B关于直线AC的对称点F,连接DF交AC于点E,由(1)得,抛物线解析式为![]() ①,∴D(0,﹣4),∵点C是直线y=﹣x+4②与抛物线的交点,∴联立①②得:
①,∴D(0,﹣4),∵点C是直线y=﹣x+4②与抛物线的交点,∴联立①②得: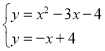 ,解得,
,解得,![]() (舍)或
(舍)或![]() ,∴C(﹣2,6),∵A(4,0),∴直线AC解析式为y=﹣x+4,∵直线BF⊥AC,且B(﹣1,0),∴直线BF解析式为y=x+1,设点F(m,m+1),∴G(
,∴C(﹣2,6),∵A(4,0),∴直线AC解析式为y=﹣x+4,∵直线BF⊥AC,且B(﹣1,0),∴直线BF解析式为y=x+1,设点F(m,m+1),∴G(![]() ,
,![]() ),∵点G在直线AC上,∴
),∵点G在直线AC上,∴![]() ,∴m=4,∴F(4,5),∵D(0,﹣4),∴直线DF解析式为
,∴m=4,∴F(4,5),∵D(0,﹣4),∴直线DF解析式为![]() ,∵直线AC解析式为y=﹣x+4,∴直线DF和直线AC的交点E(
,∵直线AC解析式为y=﹣x+4,∴直线DF和直线AC的交点E(![]() ,
,![]() );
);
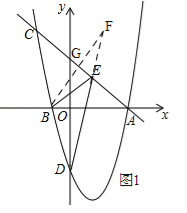
(3)∵BD=![]() ,由(2)有,点B到线段AC的距离为BG=
,由(2)有,点B到线段AC的距离为BG=![]() BF=
BF=![]() ×
×![]() =
=![]() >BD,∴∠BED不可能是直角,∵B(﹣1,0),D(0,﹣4),∴直线BD解析式为y=﹣4x+4,∵△BDE为直角三角形,∴∠BDE=90°或∠BDE=90°.
>BD,∴∠BED不可能是直角,∵B(﹣1,0),D(0,﹣4),∴直线BD解析式为y=﹣4x+4,∵△BDE为直角三角形,∴∠BDE=90°或∠BDE=90°.
①当∠BDE=90°时, BE⊥BD交AC于B,∴直线BE解析式为![]() ,∵点E在直线AC:y=﹣x+4的图象上,∴E(3,1);
,∵点E在直线AC:y=﹣x+4的图象上,∴E(3,1);
当②∠BDE=90°时,BE⊥BD交AC于D,∴直线BE的解析式为![]() ,∵点E在抛物线
,∵点E在抛物线![]() 上,∴直线BE与抛物线的交点为(0,﹣4)和(
上,∴直线BE与抛物线的交点为(0,﹣4)和(![]() ,
,![]() ),∴E(
),∴E(![]() ,
,![]() ),即:满足条件的点E的坐标为E(3,1)或(
),即:满足条件的点E的坐标为E(3,1)或(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】重庆一中渝北分校积极组织学生开展课外阅读活动,为了解全校学生每周课外阅读的时间量t(单位:小时),采用随机抽样的方法抽取部分学生进行了问卷调查,调查结果按0≤t<2,2≤t<3,3≤t<4,t≥4分为四个等级,并分别用A、B、C、D表示,根据调查结果统计数据绘制成了如图所示的两幅不完整的统计图,由图中给出的信息解答下列问题: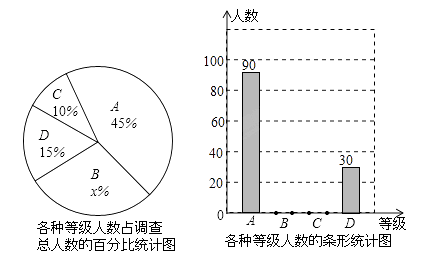
(1)求这次抽查的学生总数是多少人,并求出x的值;
(2)将不完整的条形统计图补充完整;
(3)若该校共有学生3600人,试估计每周课外阅读时间量满足2≤t<4的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某品牌汽车生产厂为了占领市场提高销售量,对经销商采取销售奖励活动,在2014年10月前奖励办法以下表计算奖励金额,2014年10月后以新奖励办法执行.某经销商在新奖励办法出台前一个月共售出某品牌汽车的A型和B型共413台,新奖励办法出台后的第一个月售出这两种型号的汽车共510台,其中A型和B型汽车的销售量分别比新奖励办法出台前一个月增长25%和20%.2014年10月前奖励办法:
销售量(x台) | 每台奖励金额(元) |
0<x≤ 100 | 200 |
100<x≤300 | 500 |
x>300 | 1000 |
(1)在新办法出台前一个月,该经销商共获得奖励金额多少元?
(2)在新办法出台前一个月,该经销商销售的A型和B型汽车分别为多少台?
(3)若A型汽车每台售价为10万元,B型汽车每台售价为12万元.新奖励办法是:每销售一台A型汽车按每台汽车售价的 ![]() 给予奖励,每销售一台B型汽车按每台汽车售价的
给予奖励,每销售一台B型汽车按每台汽车售价的 ![]() 给予奖励.新奖励办法出台后的第二个月,A型汽车的销售量比出台后的第一个月增加了
给予奖励.新奖励办法出台后的第二个月,A型汽车的销售量比出台后的第一个月增加了 ![]() ;而B型汽车受到某问题零件召回的影响,销售量比出台后的第一个月减少了
;而B型汽车受到某问题零件召回的影响,销售量比出台后的第一个月减少了 ![]() ,新奖励办法出台后的第二个月该经销商共获得的奖励金额355680元,求
,新奖励办法出台后的第二个月该经销商共获得的奖励金额355680元,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等边△ABC的顶点B,C的坐标分别为(2,0),(6,0),点N从A点出发沿AC向C点运动,连接ON交AB于点M,当点M恰平分线段ON时,求线段CN的长. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,直线![]() 与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
与x轴、y轴相交于B、C两点,动点D在线段OB上,将线段DC绕着点D顺时针旋转90°得到DE,过点E作直线l⊥x轴于H,过点C作CF⊥y轴,交直线l于F,设点D的横坐标为m.
(1)请直接写出点B、C的坐标;
(2)当点E落在直线BC上时,求tan∠FDE的值;
(3)对于常数m,探究:在直线l上是否存在点G,使得∠CDO=∠DFE+∠DGH?若存在,请求出点G的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com