
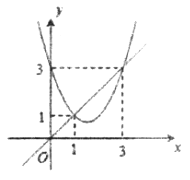
【题目】函数![]() 与
与![]() 的图象如图所示,有以下结论:①
的图象如图所示,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④当
;④当![]() 时,
时,![]() .其中正确的结论有( )
.其中正确的结论有( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
【解析】
由函数y=x2+bx+c与x轴无交点,可得b2-4c<0;当x=1时,y=1+b+c=1;当x=3时,y=9+3b+c=3;当1<x<3时,二次函数值小于一次函数值,可得x2+bx+c<x,继而可求得答案.
①由图象可知:抛物线与x轴无交点,即△<0,∴△=b2-4ac<0,故此选项错误;
②由图象可知:抛物线过点(1,1)即当x=1时,y=a+b+c=1,
a+b+c+1=2>0,故此选项正确;
③由点(3,3)在抛物线上,得到9a+3b+c=3,
∴9a+3b+c+3=6>0,正确;
④由图象可知,当1<x<3时,抛物线在直线y=kx的下方,
即当1<x<3时,x2+bx+c<kx,
∴x2+(b-k)x+c<0,故此选项正确.
故选C.


 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案科目:初中数学 来源: 题型:
【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下列结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=![]() .其中正确的结论有 ( )
.其中正确的结论有 ( )

A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
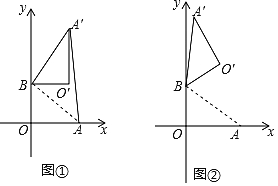
【题目】在平面直角坐标系中,O为原点,点A(4,0),点B(0,3),把△ABO绕点B逆时针旋转得到△A′BO′,点A、O旋转后的对应点为A′、O′,记旋转角为α.
(1)如图①,若α=90°,求AA′的长;
(2)如图②,若α=120°,求点O′的坐标;
(3)记K为AB的中点,S为△KA′O′的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
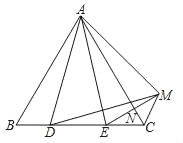
【题目】如图,△ABC是等边三角形,D,E是BC上的两点,且BD=CE,连接AD、AE,将△AEC沿AC翻折,得到△AMC,连接EM交AC于点N,连接DM.以下判断:①AD=AE,②△ABD≌△DCM,③△ADM是等边三角形,④CN=![]() EC中,正确的是_____.
EC中,正确的是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
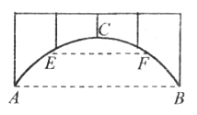
【题目】廊桥是我国古老的文化遗产,如图,是某座抛物线型的廊桥示意图.已知水面AB宽40米,抛物线最高点C到水面AB的距离为10米,为保护廊桥的安全,在该抛物线上距水面AB高为8米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)
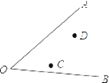
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为8的等边三角形,P是AC边上一动点,由A向C运动(与A、C不重合),Q是CB延长线上一点,与点P同时以相同的速度由B向CB延长线方向运动(点Q不与点B重合),过P作PE⊥AB于E,连接PQ交AB于D,在运动的过程中线段ED的长为( )
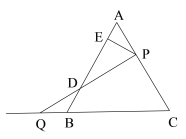
A.1.5B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,Rt△ABE≌Rt△ECD,点B、E、C在同一直线上,则结论:①AE=ED;②AE⊥DE;③BC=AB+CD;④AB∥DC中成立的是( )
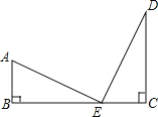
A. 仅① B. 仅①③ C. 仅①③④ D. 仅①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com