
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)
【答案】见详解.
【解析】
由所求的点P满足PC=PD,利用线段垂直平分线定理得到P点在线段CD的垂直平分线上,再由点P到∠AOB的两边的距离相等,利用角平分线定理得到P在∠AOB的角平分线上,故作出线段CD的垂直平分线,作出∠AOB的角平分线,两线交点即为所求的P点.
解:如图所示: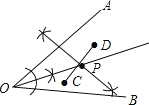
作法:(1)以O为圆心,任意长为半径画弧,与OA、OB分别交于两点;
(2)分别以这两交点为圆心,大于两交点距离的一半长为半径,在角内部画弧,两弧交于一点;
(3)以O为端点,过角内部的交点画一条射线;
(4)连接CD,分别为C、D为圆心,大于![]() CD长为半径画弧,分别交于两点;
CD长为半径画弧,分别交于两点;
(5)过两交点画一条直线;
(6)此直线与前面画的射线交于点P,
∴点P为所求的点.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AD∥BC,点M是AD的中点,若动点N从点B出发沿边BC方向向终点C运动,连结BM,CM,AN,DN,则在整个运动过程中,阴影部分面积和的大小变化情况是( )

A.不变B.一直变大C.先减小后增大D.先增大后减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某博物馆 7 天假期中每题游客人数的变化情况如下表:
(9 月 30 日的游客人数为 3 万)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人数变化 (单位:万) | +1.2 | +0.9 | +0.5 | -0.5 | -0.9 | +0.2 | -1.2 |
(注:“+”表示比前一天的人数增加,“—”表示比前一天的人数减少)
(1)求出 10 月 2 日游客人数
(2)请判断 7 天内游客人数最多的是哪天,最少的是哪天,它们相差是多少?
(3)以 9 月 30 日的游客人数为 3 万为零点,用折线统计图表示这 7 天游客人数情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学习兴趣小组参加一次单元测验,成绩统计情况如下表.
分 数 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 82 | 83 | 84 | 86 | 88 | 90 | 92 |
人 数 | 1 | 1 | 5 | 4 | 3 | 2 | 3 | 1 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)该兴趣小组有多少人?
(2)兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少?
(3)老师打算为兴趣小组下单元考试设定一个新目标,学生达到或超过目标给予奖励,并希望小组 三分之一左右的优秀学生得到奖励,请你帮老师从平均数、中位数、众数三个数中选择一个比较恰 当的目标数;如果计划让一半左右的人都得到奖励,确定哪个数作为目标恰当些?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
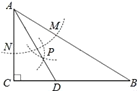
①AD是∠BAC的平分线;②∠ADC=60°; ③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
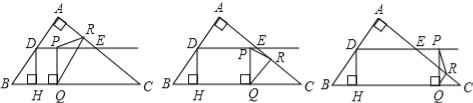
(1)求点D到BC的距离DH的长;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录的是今年长江某一周内的水位变化情况,这一周的上周末的水位已达到警戒水位![]() 米(正号表示水位比前一天上升,负号表示水位比前一天下降).
米(正号表示水位比前一天上升,负号表示水位比前一天下降).
星期 | 一 | 二 | 三 | 四 | 五 | 六 |
水位 变化(米) | +0.2 |
| -0.4 |
| +0.3 |
|
(1)本周哪一天长江的水位最高?位于警戒水位之上还是之下?
(2)与上周周末相比,本周周末长江的水位是上升了还是下降了?并通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保护环境,我市公交公司计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元.
(1)求购买A型和B型公交车每辆各需多少万元?
(2)预计在某线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次.若该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案?
(3)在(2)的条件下,哪种购车方案总费用最少?最少总费用是多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com