
【题目】某学习兴趣小组参加一次单元测验,成绩统计情况如下表.
分 数 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 82 | 83 | 84 | 86 | 88 | 90 | 92 |
人 数 | 1 | 1 | 5 | 4 | 3 | 2 | 3 | 1 | 1 | 1 | 2 | 3 | 1 | 2 |
(1)该兴趣小组有多少人?
(2)兴趣小组本次单元测试成绩的平均数、中位数、众数各是多少?
(3)老师打算为兴趣小组下单元考试设定一个新目标,学生达到或超过目标给予奖励,并希望小组 三分之一左右的优秀学生得到奖励,请你帮老师从平均数、中位数、众数三个数中选择一个比较恰 当的目标数;如果计划让一半左右的人都得到奖励,确定哪个数作为目标恰当些?
【答案】(1)30;(2)平均数为80.3;中位数是78; 众数是75;(3)如果希望小组三分之一左右的优秀学生得到奖励,老师可以选择平均数;如果计划让一半左右的人都得到奖励,确定中位数作为目标恰当些.
【解析】
(1)将各分数人数相加即可;
(2)根据平均数、中位数、众数的定义求解即可;
(3)根据(2)中数据即可得出;如果计划让一半左右的人都得到奖励,确定中位数作为目标恰当些,因为中位数以上的人数占总人数的一半左右.
(1)该兴趣小组人数为:1+1+5+4+3+2+3+1+1+1+2+3+1+2=30;
(2)本次单元测试成绩的平均数为:![]() (73+74+75×5+76×4+77×3+78×2+79×3+82+83+84+86×2+88×3+90+92×2)=80.3(分),
(73+74+75×5+76×4+77×3+78×2+79×3+82+83+84+86×2+88×3+90+92×2)=80.3(分),
表格中数据已经按照从小到大的顺序排列,一共有30个数,位于第15、第16的数都是78,所以中位数是(78+78)÷2=78(分),
75出现了5次,次数最多,所以众数是75分;
(3)由(2)可知,平均数为80.3分,中位数为78分,众数为75分,如果希望小组三分之一左右的优秀学生得到奖励,老师可以选择平均数;如果计划让一半左右的人都得到奖励,确定中位数作为目标恰当些,因为中位数以上的人数占总人数的一半左右.


科目:初中数学 来源: 题型:
【题目】如图,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF∥AB交AC于F.

(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数![]() (k≠0)的图象经过
(k≠0)的图象经过![]() ,
, ![]() 两点,二次函数
两点,二次函数![]() (其中a>2).
(其中a>2).

(1)求一次函数的表达式及二次函数图象的顶点坐标(用含a的代数式表示);
(2)利用函数图象解决下列问题:
①若![]() ,求当
,求当![]() 且
且![]() ≤0时,自变量x的取值范围;
≤0时,自变量x的取值范围;
②如果满足![]() 且
且![]() ≤0时的自变量x的取值范围内恰有一个整数,直接写出a的取值范围.
≤0时的自变量x的取值范围内恰有一个整数,直接写出a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】权威市调机构IDC发布了2018年第四季度全球智能手机出货量报告如下表:
手机品牌 | 2018年第四季度市场出货量(万台) | 2018年第四季度市场份额 | 2017年第四季度市场出货量(万台) | 2017年第四季度市场份额 |
Samsung | 70.4 | 18.7% | 74.5 | 18.9% |
Apple | 68.4 | 18.2% | 77.3 | 19.6% |
Huawei | 60.5 | 16.1% | 42.1 | 10.7% |
Xiaomi | 29.2 | 7.8% | 27.3 | 6.9% |
HMDGlobal | 28.6 | 7.6% | 28.2 | 7.1% |
Others | 118.4 | 31.5% | 145.3 | 36.8% |
总计 | 75.4 | 100.0% | 394.6 | 100.0% |
根据上表数据得出以下推断,其中结论正确的是( )
A.Huawei和Xiaomi2018年第四季度市场份额总和达到25%
B.2018年第四季度比2017年第四季度市场份额增幅最大的是Apple手机
C.Huawei手机2018年第四季度比2017年第四季度市场出货量增加18.4万合
D.2018年第四季度全球智能手机出货量同比下降约10%
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
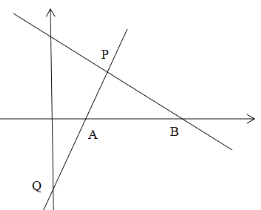
【题目】在平面直角坐标系中,直线y1=kx+b经过点P(2,2)和点Q(0,﹣2),与x轴交于点A,与直线y2=mx+n交于点P.
(1)求出直线y1=kx+b的解析式;
(2)当m<0时,直接写出y1<y2时自变量x的取值范围;
(3)直线y2=mx+n绕着点P任意旋转,与x轴交于点B,当△PAB是等腰三角形时,点B有几种位置?请你分别求出点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
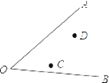
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1解析式为y=2x﹣2,且直线l1与x轴交于点D,直线l2与y轴交于点A,且经过点B(3,1),直线l1、l2交于点C(2,2).
(1)求直线l2的解析式;
(2)根据图象,求四边形OACD的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AD是BC边上的高,AE、BF分别是∠BAC、∠ABC的平分线,∠BAC=50°,∠ABC=60°,则∠EAD+∠ACD=( )

A. 75° B. 80° C. 85° D. 90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com