
°æƒø°ø»ÁÕº£¨‘⁄Rt°˜ABC÷–£¨°œA=90°„£¨AB=6£¨AC=8£¨D£¨E∑÷± «±þAB£¨ACµƒ÷–µ„£¨µ„P¥”µ„D≥ˆ∑¢—ÿDE∑ΩœÚ‘À∂Ø£¨π˝µ„P◊˜PQ°ÕBC”⁄Q£¨π˝µ„Q◊˜QR°ŒBAΩªAC”⁄R£¨µ±µ„Q”ε„C÷ÿ∫œ ±£¨µ„PÕ£÷π‘À∂أƅËBQ=x£¨QR=y£Æ
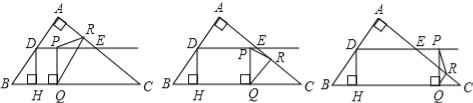
£®1£©«Ûµ„DµΩBCµƒæý¿ÎDHµƒ≥§£ª
£®2£©«Ûyπÿ”⁄xµƒ∫Ø ˝πÿœµ Ω£®≤ª“™«Û–¥≥ˆ◊‘±‰¡øµƒ»°÷µ∑∂Œß£©£ª
£®3£© «∑ҥʑ⁄µ„P£¨ π°˜PQRŒ™µ»—¸»˝Ω«–Œ£ø»Ù¥Ê‘⁄£¨«Î«Û≥ˆÀ˘”–¬˙◊„“™«Ûµƒxµƒ÷µ£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
°æ¥∞∏°ø£®1£©![]() £®2£©y=-
£®2£©y=-![]() x+6£®3£©¥Ê‘⁄£¨
x+6£®3£©¥Ê‘⁄£¨![]() ªÚ6ªÚ
ªÚ6ªÚ![]()
°æΩ‚Œˆ°ø
‘Â∑÷Œˆ£∫£®1£©∏˘æð»˝Ω«–ŒœýÀ∆µƒ≈–∂®∂®¿Ì«Û≥ˆ°˜BHD°◊°˜BAC£¨∏˘æðœýÀ∆»˝Ω«–Œµƒ–‘÷ «Û≥ˆDHµƒ≥§£ª
£®2£©∏˘æð°˜RQC°◊°˜ABC£¨∏˘æð»˝Ω«–ŒµƒœýÀ∆±»«Û≥ˆyπÿ”⁄xµƒ∫Ø ˝πÿœµ Ω£ª
£®3£©ª≠≥ˆÕº–Œ£¨∏˘æðÕº–ŒΩ¯––Ã÷¬€£∫
¢Ÿµ±PQ=PR ±£¨π˝µ„P◊˜PM°ÕQR”⁄M£¨‘ÚQM=RM£Æ”…”⁄°œ1+°œ2=90°„£¨°œC+°œ2=90°„£¨°ý°œ1=°œC£Æ
°ýcos°œ1=cosC=![]() £¨°ý
£¨°ý![]() £¨º¥ø…«Û≥ˆxµƒ÷µ£ª
£¨º¥ø…«Û≥ˆxµƒ÷µ£ª
¢⁄µ±PQ=RQ ±£¨©Å![]() x+6=
x+6=![]() £¨x=6£ª
£¨x=6£ª
¢€µ±PR=QR ±£¨‘ÚRŒ™PQ÷–¥πœþ…œµƒµ„£¨”⁄ «µ„RŒ™ECµƒ÷–µ„£¨π CR=![]() CE=
CE=![]() AC=2£Æ”…”⁄tanC=
AC=2£Æ”…”⁄tanC=![]() £¨x=
£¨x=![]() £Æ
£Æ
‘Ã‚Ω‚Œˆ£∫£®1£©‘⁄Rt°˜ABC÷–£¨
°þ°œA=90°„£¨AB=6£¨AC=8£¨
°ýBC=![]() =10£Æ
=10£Æ
°þ°œDHB=°œA=90°„£¨°œB=°œB£Æ
°ý°˜BHD°◊°˜BAC£¨
°ý![]() £¨
£¨
°ýDH=![]() AC=
AC=![]() °¡8=
°¡8=![]()
£®2£©°þQR°ŒAB£¨
°ý°œQRC=°œA=90°„£Æ
°þ°œC=°œC£¨
°ý°˜RQC°◊°˜ABC£¨
°ý![]() £¨°ý
£¨°ý![]() £¨
£¨
º¥yπÿ”⁄xµƒ∫Ø ˝πÿœµ ΩŒ™£∫y=-![]() x+6£Æ
x+6£Æ
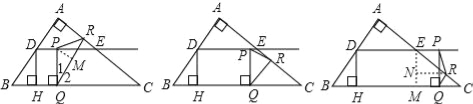
£®3£©¥Ê‘⁄£¨∑÷»˝÷÷«Èøˆ£∫
¢Ÿµ±PQ=PR ±£¨π˝µ„P◊˜PM°ÕQR”⁄M£¨‘ÚQM=RM£Æ
°þ°œ1+°œ2=90°„£¨°œC+°œ2=90°„£¨
°ý°œ1=°œC£Æ
°ýcos°œ1=cosC=![]() £¨
£¨
°ý![]() £¨
£¨
°ý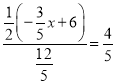 £¨
£¨
°ýx=![]() £Æ
£Æ
¢⁄µ±PQ=RQ ±£¨©Å![]() x+6=
x+6=![]() £¨
£¨
°ýx=6£Æ
¢€◊˜EM°ÕBC£¨RN°ÕEM£¨
°ýEM°ŒPQ£¨
µ±PR=QR ±£¨‘ÚRŒ™PQ÷–¥πœþ…œµƒµ„£¨
°ýEN=MN£¨
°ýER=RC£¨
°ýµ„RŒ™ECµƒ÷–µ„£¨
°ýCR=![]() CE=
CE=![]() AC=2£Æ
AC=2£Æ
°þtanC=![]() £¨
£¨
°ý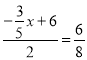 £¨
£¨
°ýx=![]() £Æ
£Æ
◊€…œÀ˘ ˆ£¨µ±xŒ™![]() ªÚ6ªÚ
ªÚ6ªÚ![]() ±£¨°˜PQRŒ™µ»—¸»˝Ω«–Œ£Æ
±£¨°˜PQRŒ™µ»—¸»˝Ω«–Œ£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø“—÷™∂˛¥Œ∫Ø ˝y=mx2+nx+pÕºœÛµƒ∂•µ„∫·◊¯±Í «2£¨”Îx÷·Ωª”⁄A£®x1£¨0£©°¢B£®x2£¨0£©£¨x1£º0£ºx2£¨”Îy÷·Ωª”⁄µ„C£¨OŒ™◊¯±Í‘≠µ„£¨tan°œCAO©Åtan°œCBO=1£Æ
£®1£©«Û÷§£∫n+4m=0£ª
£®2£©«Ûm°¢nµƒ÷µ£ª
£®3£©µ±p£æ0«“∂˛¥Œ∫Ø ˝ÕºœÛ”Î÷±œþy=x+3Ωˆ”–“ª∏ˆΩªµ„ ±£¨«Û∂˛¥Œ∫Ø ˝µƒ◊Ó¥Û÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øπÿ”⁄“ª◊È ˝æðµƒ∆Ωæ˘ ˝°¢÷–Œª ˝°¢÷⁄ ˝£¨œ¬¡–Àµ∑®÷–’˝»∑µƒ «£∫
A. ∆Ωæ˘ ˝“ª∂® «’‚◊È ˝÷–µƒƒ≥∏ˆ ˝ B. ÷⁄ ˝“ª∂® «’‚◊È ˝÷–µƒƒ≥∏ˆ ˝
C. ÷–Œª ˝“ª∂® «’‚◊È ˝÷–µƒƒ≥∏ˆ ˝ D. “‘…œÀµ∑®∂º≤ª∂‘
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øƒ≥◊‘»ª±£ª§«¯µƒ√ʪ˝Œ™2150 000 000∆Ω∑Ω√◊£¨2150000000’‚∏ˆ ˝”√ø∆—ߺ∆ ˝∑®±Ì 挙£∫
A. 2.15°¡108 B. 21.5°¡108 C. 2.15°¡109 D. 0.215°¡109
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øœ¬¡–√¸Ã‚÷–¥ÌŒÛµƒ”–£®°°°°£©∏ˆ
£®1£©µ»—¸»˝Ω«–Œµƒ¡Ω∏ˆµ◊Ω«œýµ»°°
£®2£©∂‘Ω«œþœýµ»«“ª•œý¥π÷±µƒÀƒ±þ–Œ «’˝∑Ω–Œ
£®3£©∂‘Ω«œþœýµ»µƒÀƒ±þ–ŒŒ™æÿ–Œ°°
£®4£©‘≤µƒ«–œþ¥π÷±”⁄∞Îæ∂
£®5£©∆Ω∑÷œ“µƒ÷±æ∂¥π÷±”⁄œ“
A. 1 B. 2 C. 3 D. 4
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°øæÿ–Œ°¢¡‚–Œ∫Õ’˝∑Ω–Œµƒ∂‘Ω«œþ∂ºæþ”–µƒ–‘÷ «£®°°°°£©
A. ª•œý∆Ω∑÷B. ª•œý¥π÷±C. œýµ»D. »Œ∫Œ“ªÃı∂‘Ω«œþ∆Ω∑÷“ª◊È∂‘Ω«
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø∏˘æ𜬡–Ãıº˛ø…¡–≥ˆ“ª‘™“ª¥Œ∑Ω≥õƒ «(°° °°)
A. a”Î1µƒ∫Õµƒ3±∂
B. º◊ ˝µƒ2±∂”Γ“ ˝µƒ3±∂µƒ∫Õ
C. a”Îbµƒ≤Óµƒ20%
D. “ª∏ˆ ˝µƒ3±∂ «5
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
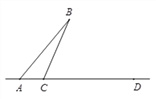
°æƒø°ø»ÁÕº£¨œþ∂ŒAB£¨ADΩª”⁄µ„A£ÆCŒ™÷±œþAD…œ“ªµ„£®≤ª”ε„A£¨D÷ÿ∫œ£©£Æπ˝µ„C‘⁄BCµƒ”“≤ý◊˜…‰œþCE°ÕBC£¨π˝µ„D◊˜÷±œþDF°ŒAB£¨ΩªCE”⁄µ„G£®G”ÎD≤ª÷ÿ∫œ£©£Æ
£®1£©»ÁÕº1£¨»Ùµ„C‘⁄œþ∂ŒAD…œ£¨«“°œBCAŒ™∂€Ω«£Æ
¢Ÿ∞¥“™«Û≤π»´Õº–Œ£ª¢⁄≈–∂œ°œB”ΰœCGDµƒ ˝¡øπÿœµ£¨≤¢÷§√˜£Æ
£®2£©»Ùµ„C‘⁄œþ∂ŒDAµƒ—”≥§œþ…œ£¨«Î÷±Ω”–¥≥ˆ°œB”ΰœCGDµƒ ˝¡øπÿœµ £ª
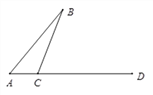
∏Ωº”£®2∑÷£©£Æ
«Îƒ„Ω·∫œ28µƒÃ‚“‚÷≥ˆ“ª∏ˆ–¬µƒÕÿ’πŒ  £Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com