
【题目】已知二次函数y=mx2+nx+p图象的顶点横坐标是2,与x轴交于A(x1,0)、B(x2,0),x1<0<x2,与y轴交于点C,O为坐标原点,tan∠CAO﹣tan∠CBO=1.
(1)求证:n+4m=0;
(2)求m、n的值;
(3)当p>0且二次函数图象与直线y=x+3仅有一个交点时,求二次函数的最大值.
【答案】(1)证明见解析(2)m=![]() ,n=-1或m=-
,n=-1或m=-![]() ,n=1(3)4
,n=1(3)4
【解析】
试题分析:(1)由题意可知抛物线的对称轴为x=2,利用对称轴公式x=![]() ,易证n+4m=0;
,易证n+4m=0;
(2)本问利用三角函数定义和抛物线与x轴交点坐标性质求解.特别需要注意的是抛物线的开口方向未定,所以所求m、n的值将有两组,不能遗漏;
(3)本问利用一元二次方程的判别式等于0求解.当p>0时,m、n的值随之确定;将抛物线的解析式与直线的解析式联立,得到一个一元二次方程;由交点唯一可知,此一元二次方程的判别式等于0,据此求出p的值,从而确定了抛物线的解析式;最后由抛物线的解析式确定其最大值.
试题解析:
(1)∵二次函数y=mx2+nx+p图象的顶点横坐标是2,
∴抛物线的对称轴为x=2,
即![]() =2,
=2,
化简得:n+4m=0.
(2)∵二次函数y=mx2+nx+p与x轴交于A(x1,0)、B(x2,0),x1<0<x2,
∴OA=﹣x1,OB=x2;
x1+x2=![]() ,x1x2=
,x1x2=![]() ;
;
令x=0,得y=p,
∴C(0,p),
∴OC=|p|.
由三角函数定义得:tan∠CAO=![]() ,tan∠CBO=
,tan∠CBO=![]() .
.
∵tan∠CAO﹣tan∠CBO=1
,即![]() ,
,
化简得:![]() =
=![]() ,
,
将x1+x2=![]() ,x1x2=
,x1x2=![]() 代入得:
代入得: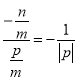 ,
,
化简得:n=![]() =±1.
=±1.
由(1)知n+4m=0,
∴当n=1时,m=-![]() ;当n=﹣1时,m=
;当n=﹣1时,m=![]() .
.
∴m、n的值为:m=![]() ,n=﹣1(此时抛物线开口向上)或m=-
,n=﹣1(此时抛物线开口向上)或m=-![]() ,n=1(此时抛物线开口向下).
,n=1(此时抛物线开口向下).
(3)解:由(2)知,当p>0时,n=1,m=-![]() ,
,
∴抛物线解析式为:y=![]() x2+x+p.
x2+x+p.
联立抛物线y=![]() x2+x+p与直线y=x+3解析式得到:
x2+x+p与直线y=x+3解析式得到: ![]() x2+x+p=x+3,
x2+x+p=x+3,
化简得:x2﹣4(p﹣3)=0 ①.
∵二次函数图象与直线y=x+3仅有一个交点,
∴一元二次方程①的判别式等于0,
即△=02+16(p﹣3)=0,解得p=3.
∴抛物线解析式为:y=![]() x2+x+p=y=
x2+x+p=y=![]() x2+x+3=
x2+x+3=![]() (x﹣2)2+4,
(x﹣2)2+4,
当x=2时,二次函数有最大值,最大值为4.
∴当p>0且二次函数图象与直线y=x+3仅有一个交点时,二次函数的最大值为4.


 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
【题目】如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.

(1)写出y与t之间的函数关系式.
(2)通话2分钟应付通话费多少元?
(3)通话7分钟呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我市“新媒体”课堂比赛中,7位评委给某位选手的评分不完全相同,若去掉一个最高分,去掉一个最低分,则以下四个统计量中一定不会发生变化的是( )
A. 平均分B. 众数C. 中位数D. 极差
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列判断正确的是( )
A. 若|a|=|b|,则a=b B. 若|a|=|b|,则a= -b
C. 若a=b,则|a|=|b| D. 若a=-b,则|a|= -|b|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠A=90°,AB=6,AC=8,D,E分别是边AB,AC的中点,点P从点D出发沿DE方向运动,过点P作PQ⊥BC于Q,过点Q作QR∥BA交AC于R,当点Q与点C重合时,点P停止运动.设BQ=x,QR=y.
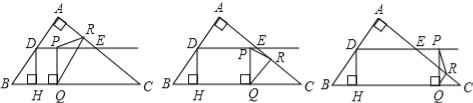
(1)求点D到BC的距离DH的长;
(2)求y关于x的函数关系式(不要求写出自变量的取值范围);
(3)是否存在点P,使△PQR为等腰三角形?若存在,请求出所有满足要求的x的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com