
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
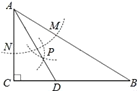
①AD是∠BAC的平分线;②∠ADC=60°; ③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A. 1B. 2C. 3D. 4
【答案】D
【解析】
根据角平分线的作法可得①正确,再根据三角形内角和定理和外角与内角的关系可得∠ADC=60°,再根据线段垂直平分线的性质逆定理可得③正确,根据直角三角形的性质得出AD=2CD,再由线段垂直平分线的性质得出AD=BD,进而可得④正确.
解:由题意可知AD是∠BAC的平分线,故①正确;
∵∠C=90°,∠B=30°,
∴∠CAB=60°,
∵AD平分∠CAB,
∴∠DAB=∠DAC= 30°,
∴∠ADC=30°+30°=60°,故②正确;
∵∠DAB=30°,∠B=30°,
∴AD=BD,
∴点D在AB的中垂线上,故③正确;
∵∠CAD=30°,
∴AD=2CD.
∵点D在AB的中垂线上,
∴AD=BD,
∵∠DAC= 30°,∠C=90°,
∴AD=2CD,BC=3CD
∴S△DAC:S△ABC=1:3,故④正确.
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
科目:初中数学 来源: 题型:
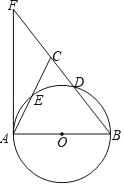
【题目】如图,AB是⊙O的直径,D是⊙O上一点,点E是AC的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
(1)求证:AB=BC;
(2)如果AB=5,tan∠FAC=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.
如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位秒的速度沿着折线数抽”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.当点P到达点C时,两点都停上远动.设运动的时间为1秒.问:
(1)t=2秒时,点P在“折线数轴”上所对应的数是_______;点P到点Q的距离是_____单位长度;
(2)动点P从点4运动至C点需要_______秒;
(3)P、Q两点相遇时,求出t的值和此时相遇点M在“折线数轴”上所对应的数;
(4)如果动点P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
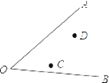
【题目】已知:∠AOB和两点C、D,求作一点P,使PC=PD,且点P到∠AOB的两边的距离相等.(要求:用尺规作图,保留作图痕迹,不写作法,不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
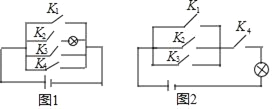
【题目】小明学习电学知识后,用四个开关按键(每个开关键闭合的可能性相等)、一个电源和一个灯泡设计了一个电路图
(1)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求任意闭合一个开关按键,灯泡能发光的概率;
(2)若小明设计的电路图(四个开关按键都处于打开状态)如图所示,求同时闭合其中的两个开关按键,灯泡能发光的概率.(用列表或树状图法)
查看答案和解析>>
科目:初中数学 来源: 题型:
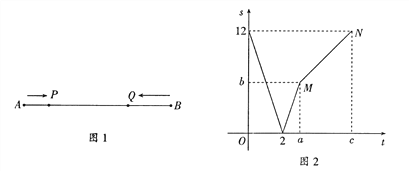
【题目】如图1,线段![]() =12厘米,动点
=12厘米,动点![]() 从点
从点![]() 出发向点
出发向点![]() 运动,动点
运动,动点![]() 从点
从点![]() 出发向点
出发向点![]()
运动,两点同时出发,到达各自的终点后停止运动.已知动点![]() 运动的速度是动点
运动的速度是动点![]() 运动的速度的2倍.设两点之间的距离为
运动的速度的2倍.设两点之间的距离为![]() (厘米),动点
(厘米),动点![]() 的运动时间为
的运动时间为![]() (秒),图2表示
(秒),图2表示![]() 与
与![]() 之间的函数关系.
之间的函数关系.
(1)求动点![]() 、
、![]() 运动的速度;
运动的速度;
(2)图2中, ![]() = ,
= , ![]() = ,
= , ![]() = ;
= ;
(3)当![]() 时,求
时,求![]() 与
与![]() 之间的函数关系式(即线段
之间的函数关系式(即线段![]() 对应的函数关系式).
对应的函数关系式).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com