
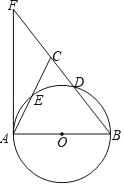
【题目】如图,AB是⊙O的直径,D是⊙O上一点,点E是AC的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
(1)求证:AB=BC;
(2)如果AB=5,tan∠FAC=![]() ,求FC的长.
,求FC的长.
【答案】(1)见解析;(2)![]() .
.
【解析】分析:(1)由AB是直径可得BE⊥AC,点E为AC的中点,可知BE垂直平分线段AC,从而结论可证;
(2)由∠FAC+∠CAB=90°,∠CAB+∠ABE=90°,可得∠FAC=∠ABE,从而可设AE=x,BE=2x,由勾股定理求出AE、BE、AC的长. 作CH⊥AF于H,可证Rt△ACH∽Rt△BAC,列比例式求出HC、AH的值,再根据平行线分线段成比例求出FH,然后利用勾股定理求出FC的值.
详解:(1)证明:连接BE.
∵AB是⊙O的直径,
∴∠AEB=90°,
∴BE⊥AC,
而点E为AC的中点,
∴BE垂直平分AC,
∴BA=BC;
(2)解:∵AF为切线,
∴AF⊥AB,
∵∠FAC+∠CAB=90°,∠CAB+∠ABE=90°,
∴∠FAC=∠ABE,
∴tan∠ABE=∠FAC=![]() ,
,
在Rt△ABE中,tan∠ABE=![]() =
=![]() ,
,
设AE=x,则BE=2x,
∴AB=![]() x,即
x,即![]() x=5,解得x=
x=5,解得x=![]() ,
,
∴AC=2AE=2![]() ,BE=2
,BE=2![]()
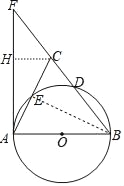
作CH⊥AF于H,如图,
∵∠HAC=∠ABE,
∴Rt△ACH∽Rt△BAC,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,
,
∴HC=2,AH=4,
∵HC∥AB,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,解得FH=
,解得FH=![]()
在Rt△FHC中,FC=![]() =
=![]() .
.


科目:初中数学 来源: 题型:
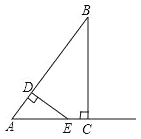
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
(1)线段AE的长为 .(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
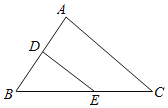
【题目】如图,在△ABC中、D、E分别是AB,BC上任意一点,连结DE,若BD=4,DE=5.
(1)BE的取值范围 ;
(2)若DE∥AC,∠A=85°,∠BED=35°,求∠B的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC⊥AB,E为⊙O上的一点,AC=EC,延长CE交AB的延长线于点D.

(1)求证:CE为⊙O的切线;
(2)若OF⊥AE,OF=1,∠OAF=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB中,AB⊥OB,且AB=OB=3,设直线![]() 截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )
截此三角形所得阴影部分的面积为S,则S与t之间的函数关系的图象为下列选项中的( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“十一”黄金周期间,某博物馆 7 天假期中每题游客人数的变化情况如下表:
(9 月 30 日的游客人数为 3 万)
日期 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
人数变化 (单位:万) | +1.2 | +0.9 | +0.5 | -0.5 | -0.9 | +0.2 | -1.2 |
(注:“+”表示比前一天的人数增加,“—”表示比前一天的人数减少)
(1)求出 10 月 2 日游客人数
(2)请判断 7 天内游客人数最多的是哪天,最少的是哪天,它们相差是多少?
(3)以 9 月 30 日的游客人数为 3 万为零点,用折线统计图表示这 7 天游客人数情况.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+3a(a>0)与x轴交于A,B两点(A在B的左侧).
(1)求抛物线的对称轴及点A,B的坐标;
(2)点C(t,3)是抛物线y=ax2﹣4ax+3a(a>0)上一点,(点C在对称轴的右侧),过点C作x轴的垂线,垂足为点D.
①当CD=AD时,求此时抛物线的表达式;
②当CD>AD时,求t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于![]() MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
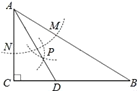
①AD是∠BAC的平分线;②∠ADC=60°; ③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织学生书法比赛,对参赛作品按A、B、C、D四个等级进行了评定.现随机取部分学生书法作品的评定结果进行分析,并绘制扇形统计图和条形统计图如下:

根据上述信息完成下列问题:
(1)求这次抽取的样本的容量;
(2)请在图②中把条形统计图补充完整;
(3)已知该校这次活动共收到参赛作品750份,请你估计参赛作品达到B级以上(即A级和B级)有多少份?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com