
【题目】在平面直角坐标系xOy中,抛物线y=ax2﹣4ax+3a(a>0)与x轴交于A,B两点(A在B的左侧).
(1)求抛物线的对称轴及点A,B的坐标;
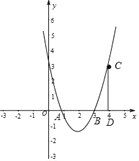
(2)点C(t,3)是抛物线y=ax2﹣4ax+3a(a>0)上一点,(点C在对称轴的右侧),过点C作x轴的垂线,垂足为点D.
①当CD=AD时,求此时抛物线的表达式;
②当CD>AD时,求t的取值范围.
【答案】(1) A(1,0),B(3,0);(2) ①y=x2﹣4x+3;②3<t<4.
【解析】分析:(1)令函数值为0得到ax2-4ax+3a=0,然后解方程可得到A点和B点坐标;利用抛物线的对称轴方程确定抛物线的对称轴;
(2)①利用点C的坐标得到CD=3,OA=t,则AD=t-1,根据题意得到t-1=3,解方程求出t得到C(4,3),然后把C点坐标代入y=ax2-4ax+3a中求出a即可得到抛物线解析式;
②利用CD>AD得到3>t-1,再利用点C在B点的右侧得到t >3,从而可确定t的范围.
详解:(1)当y=0时,ax2﹣4ax+3a=0,即x2﹣4x+3=0,解得x1=1,x2=3,
∴A(1,0),B(3,0),
抛物线的对称轴为直线x=﹣![]() =2;
=2;
(2)①∵CD⊥x轴,
∴CD=3,OD=t,
∴AD=t﹣1,
而CD=AD,
∴t﹣1=3,解得t=4,
∴C(4,3),
把C(4,3)代入y=ax2﹣4ax+3a得16a﹣16a+3a=3,解得a=1,
∴此时抛物线解析式为y=x2﹣4x+3;
②∵CD>AD,
∴3>t﹣1,
∴t<4,
而点C在点B的右侧,
∴t>3,
∴t的范围为3<t<4.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
【题目】如图,AC为⊙O的直径,B是⊙O外一点,AB交⊙O于E点,过E点作⊙O的切线,交BC于D点,DE=DC,作EF⊥AC于F点,交AD于M点。
求证:(1)BC是⊙O的切线; (2)EM=FM。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下面一列有序数对:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
A. (3,8)B. (4,7)C. (5,6)D. (6,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
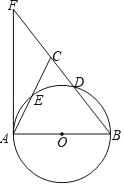
【题目】如图,AB是⊙O的直径,D是⊙O上一点,点E是AC的中点,过点A作⊙O的切线交BD的延长线于点F.连接AE并延长交BF于点C.
(1)求证:AB=BC;
(2)如果AB=5,tan∠FAC=![]() ,求FC的长.
,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)看一看下面两组式子:(3×5)2 与 32×52,[(- ![]() )×4]2 与(-
)×4]2 与(- ![]() )2×42;每组的两个算式的计算结果是否相等?
)2×42;每组的两个算式的计算结果是否相等?
(2)想一想(ab)2等于什么?猜一猜,当 n 为正整数时,(ab)n 等于什么?你能用一句 话叙述你的所得到的结果吗?
(3)运用上述结论计算下列各题
①(-8)2019×(![]() )2019
)2019
②(-1![]() )2020×(
)2020×(![]() )2020
)2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A、B两点分别在x轴、y轴上,OA=3,OB=4,连接AB.点P在平面内,若以点P、A、B为顶点的三角形与△AOB全等(点P与点O不重合),则点P的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是学习有理数的一种重要工具,任何有理数都可以用数轴上的点表示,这样能够运用数形结合的方法解决一些问题.
如图,将一条数轴在原点O和点B处各折一下,得到一条“折线数轴”.图中点A表示-10,点B表示10,点C表示18,我们称点A和点C在数轴上相距28个长度单位.动点P从点A出发,以2单位秒的速度沿着折线数抽”的正方向运动,从点O运动到点B期间速度变为原来的一半,之后立刻恢复原速;同时,动点Q从点C出发,以1单位秒的速度沿着数轴的负方向运动,从点B运动到点O期间速度变为原来的两倍,之后也立刻恢复原速.当点P到达点C时,两点都停上远动.设运动的时间为1秒.问:
(1)t=2秒时,点P在“折线数轴”上所对应的数是_______;点P到点Q的距离是_____单位长度;
(2)动点P从点4运动至C点需要_______秒;
(3)P、Q两点相遇时,求出t的值和此时相遇点M在“折线数轴”上所对应的数;
(4)如果动点P、O两点在数轴上相距的长度与Q、B两点在数轴上相距的长度相等,直接写出t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分9分)
刘卫同学在一次课外活动中,用硬纸片做了两个直角三角形,见图①、②.图①中,![]() ,
,![]() ,
,![]() ;图②中,
;图②中,![]() ,
,![]() ,
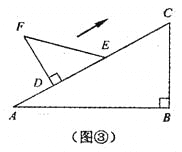
,![]() .图③是刘卫同学所做的一个实验:他将
.图③是刘卫同学所做的一个实验:他将![]() 的直角边
的直角边![]() 与
与![]() 的斜边
的斜边![]() 重合在一起,并将
重合在一起,并将![]() 沿
沿![]() 方向移动.在移动过程中,
方向移动.在移动过程中,![]() 、
、![]() 两点始终在
两点始终在![]() 边上(移动开始时点
边上(移动开始时点![]() 与点
与点![]() 重合).
重合).
(1)在![]() 沿
沿![]() 方向移动的过程中,刘卫同学发现:
方向移动的过程中,刘卫同学发现:![]() 、
、![]() 两点间的距离逐渐 ▲ .
两点间的距离逐渐 ▲ .
(填“不变”、“变大”或“变小”)
(2)刘卫同学经过进一步地研究,编制了如下问题:
问题①:当![]() 移动至什么位置,即
移动至什么位置,即![]() 的长为多少时,
的长为多少时,![]() 、
、![]() 的连线与
的连线与![]() 平行?
平行?
问题②:当![]() 移动至什么位置,即
移动至什么位置,即![]() 的长为多少时,以线段
的长为多少时,以线段![]() 、
、![]() 、
、![]() 的长度为三边长的三角形是直角三角形?
的长度为三边长的三角形是直角三角形?
问题③:在![]() 的移动过程中,是否存在某个位置,使得
的移动过程中,是否存在某个位置,使得![]() ?如果存在,
?如果存在,
求出![]() 的长度;如果不存在,请说明理由.
的长度;如果不存在,请说明理由.
请你分别完成上述三个问题的解答过程.
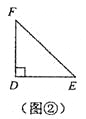
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com