
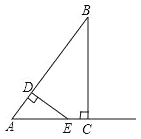
����Ŀ����ͼ����Rt��ABC�У���ACB=90����AC=3��BC=4������D�ӵ�A������ÿ��3����λ���ٶ��˶�����B������D��DE��AB������AC�ڵ�E�����D���˶�ʱ��Ϊt�루t��0����
��1���߶�AE�ij�Ϊ�� �������ú�t�Ĵ���ʽ��ʾ��
��2������ADE����ACB�������Ϊ1��4ʱ����t��ֵ��
��3������ADE����ACB�ص�����ͼ�ε��ܳ�ΪL����L��t֮��ĺ�����ϵʽ��
��4����ֱ��DE����ACB�ֳɵ�������ͼ������һ������Գ�ͼ��ʱ��ֱ��д��t��ֵ��
���𰸡���1��5t����2��![]() ����3����
����3����![]() ʱ��L=12t����
ʱ��L=12t����![]() ʱ��
ʱ�� ![]() ����4��
����4��![]() ��1��
��1��
���������������������1���������Ǻ����������2�����ݡ�ADE����ACB�������Ϊ1��4�г������������3������![]() ��
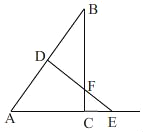
��![]() ������������� ��4����DE=CEʱ���ı���BCED����Գ�ͼ�Σ��͵�DE��BC�ཻ��F��AD=ACʱ���ı���ACFE����Գ�ͼ��������������.
������������� ��4����DE=CEʱ���ı���BCED����Գ�ͼ�Σ��͵�DE��BC�ཻ��F��AD=ACʱ���ı���ACFE����Գ�ͼ��������������.
�����������
��1����Rt��ABC��tanA=![]() =
=![]()
������ã�AD=3t��
��Rt��ADE��tanA=![]() =
=![]() =
=![]() ��
��
���ݹ��ɶ����ã�AE=5t��
�ʴ�Ϊ5t��
��2������һ����ED��AB��
���ADE=90�㣮�ߡ�ACB=90�㣬
���ACB=��ADE����A=��A��
���ABC�ס�AED��
��![]() ��
��
��AD=3t��AC=3��BC=4��
��DE=4t��
��![]() ��
��
��![]() ��
��
��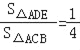 ��
��
��![]() ��
��
��![]() ���ᣩ
���ᣩ
��t��ֵΪ![]() ��
��
����������ED��AB��
���ADE=90�㣮
�ߡ�ACB=90�㣬
���ACB=��ADE��
�ߡ�A=��A��
���ABC�ס�AED��
��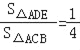 ��
��
��![]() ��
��
��AC=3��AD=3t��
��2��3t=3��t=![]() ��
��
��3���ɣ�2���ã���ABC�ס�AED��
��![]() ��
��
��AD=3t��
��DE=4t��AE=5t��BD=5��3t��
�൱![]() ʱ��L=3t+4t+5t=12t��
ʱ��L=3t+4t+5t=12t��
��L=12t��
��![]() ʱ����ͼ��
ʱ����ͼ��
�ߡ�B=��B����BDF=��BCA��
���ABC�ס�FBD��
��![]() ��
��
��BD=5��3t��
��![]() ��
��
�ߡ�BFD=��EFC����BDF=��ECF��
���B=��E��
�ߡ�FCE=��BCA
���BCA�ס�ECF��
��![]() ��
��
��CE=5t��3��
��![]() ��
��
![]() ��
��
��![]() ��
��
��4���ɣ�1��֪��AE=5t��DE=4t��
��CE=3��5t��
��DE=CEʱ���ı���BCED����Գ�ͼ�Σ�
��4t=3��5t��
��t=![]() ��
��
��DE��BC�ཻ��F��AD=ACʱ���ı���ACFE����Գ�ͼ�Σ�
��AD=3t��AC=3��
��3t=3��
��t=1��
��������������ʱ��tΪ![]() ��1��
��1��


 ���㼤�������100�ִ��Ծ�ϵ�д�
���㼤�������100�ִ��Ծ�ϵ�д� ��Ȥ������ҵ���ϿƼ�������ϵ�д�
��Ȥ������ҵ���ϿƼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
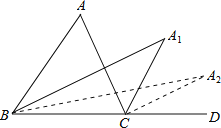
����Ŀ����ͼ,�ڡ�ABC��,��A=640,��ABC�͡�ACD��ƽ���߽��ڵ�A1,�á�A1����A1BC�͡�A1CD��ƽ���߽��ڵ�A2,�á�A2����A2BC�͡�A2CD��ƽ���߽��ڵ�A3,���A5= ______ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ʾ��һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ֳ��ĸ�С�����Σ�Ȼ��ͼ�ڵķ�ʽƴ��һ��������.
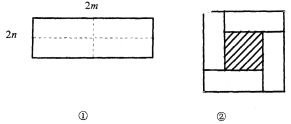
(1)����Ϊͼ���е���Ӱ���ֵ������εı߳�����_______________.
(2)�������ֲ�ͬ�ķ����д���ʽ��ʾͼ������Ӱ���ֵ����.
������___________________. ������________________.
(3)�۲�ͼ�ڣ�����д��![]() ����������ʽ֮��ĵ�����ϵ��?
����������ʽ֮��ĵ�����ϵ��?
(4)�������ϵ�����ϵ��������⣺��֪a+b=3,ab=-2,��![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
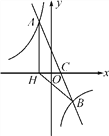
����Ŀ����ͼ����ƽ��ֱ������ϵ����һ�κ���y��ax��b(a��0)��ͼ���뷴��������y��![]() (k��0)��ͼ����A��B��������x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е���AC��4
(k��0)��ͼ����A��B��������x�ύ�ڵ�C������A��AH��x���ڵ�H����O���߶�CH���е���AC��4 ![]() ��cos��ACH��
��cos��ACH��![]() ����B������Ϊ(4��n)��
����B������Ϊ(4��n)��
(1)��÷�����������һ�κ����Ľ���ʽ��
(2)���BCH�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ʮһ���ƽ���,��ʤ�ҵ�Ǵ�������,�������һֱ����![]() �±�Ϊ������ǰһ���Ӫҵ����ǵ����
�±�Ϊ������ǰһ���Ӫҵ����ǵ����![]() ��֪9��30�յ�Ӫҵ��Ϊ26��Ԫ��
��֪9��30�յ�Ӫҵ��Ϊ26��Ԫ��
10��1�� | 2�� | 3�� | 4�� | 5�� | 6�� | 7�� |
4 | 3 | 2 | 0 |
|
|
|
![]() �ƽ�����������͵���һ�죿
�ƽ�����������͵���һ�죿![]() ֱ�ӻش�,����д����
ֱ�ӻش�,����д����![]() ��
��
![]() �ƽ�����ƽ��ÿ���Ӫҵ���Ƕ��٣�
�ƽ�����ƽ��ÿ���Ӫҵ���Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����![]() ����
����![]() ����
����![]() ��
�� ![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���˶������㡣��
���˶������㡣��![]() �Ե�
�Ե�![]() ��������
��������![]() ���ٶ���
���ٶ���![]() �����˶���ͬʱ��
�����˶���ͬʱ�� ![]() �Ե�
�Ե�![]() ������
������![]() ���ٶ���
���ٶ���![]() �����˶�����____________�룬��
�����˶�����____________�룬��![]() ��
��![]() ��
��![]() �������������
�������������![]() ������
������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ACΪ��O��ֱ����B����O��һ�㣬AB����O��E�㣬��E������O�����ߣ���BC��D�㣬DE��DC����EF��AC��F�㣬��AD��M�㡣
��֤����1��BC����O�����ߣ� ��2��EM��FM��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
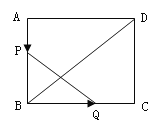
����Ŀ����ͼ����P����AOB������һ�㣬OP=5cm����M�͵�N�ֱ�������OA������OB�ϵĶ��㣬��PMN�ܳ�����Сֵ��5cm������AOB�Ķ����ǣ�������

A. 25�� B. 30�� C. 35�� D. 40��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
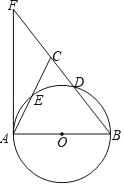
����Ŀ����ͼ��AB�ǡ�O��ֱ����D�ǡ�O��һ�㣬��E��AC���е㣬����A����O�����߽�BD���ӳ����ڵ�F������AE���ӳ���BF�ڵ�C��
��1����֤��AB=BC��
��2�����AB=5��tan��FAC=![]() ����FC�ij���
����FC�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com