
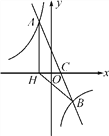
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 ![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
【答案】(1)y=-![]() ,y=-2x +4;(2)8
,y=-2x +4;(2)8
【解析】试题分析:(1)首先利用锐角三角函数关系得出HC的长,再利用勾股定理得出AH的长,即可得出A点坐标,进而求出反比例函数解析式,再求出B点坐标,即可得出一次函数解析式;
(2)利用B点坐标的纵坐标再利用HC的长即可得出△BCH的面积.
试题解析:
(1)∵AH⊥x轴于点H,
∴∠AHC=90°,
∴CH=AC·cos∠ACH=4![]() ×
×![]() =4,
=4,
∴AH=![]() =8,
=8,
又∵点O是CH的中点,
∴CO=OH=![]() CH=2,
CH=2,
∴点C(2,0),H(-2,0) ,A(-2,8),
把A(-2,8)代入反比例函数的解析式中,得k=-16,
∴反比例函数的解析式为y=-![]() ,
,
把A(-2,8),C(2,0)代入一次函数解析式中,得
![]() 解得
解得![]()
∴一次函数的解析式为y=-2x +4;
(2)将B(4,n)代入y=-![]() 中,得n=-4,
中,得n=-4,
∴S△BCH=![]() ·CH·|yB|=
·CH·|yB|=![]() ×4×4=8.
×4×4=8.


科目:初中数学 来源: 题型:
【题目】从2开始,连续的偶数相加,它们和的情况如下表:
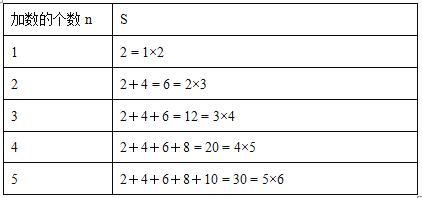
(1)当n=6时, S的值为__________.
(2)根据上题的规律计算:26+28+30+…+60的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发向右运动,运动时间为t秒.

(1)若运动2秒时,则点P表示的数为_______,点P、Q之间的距离是______个单位;
(2)求经过多少秒后,点P、Q重合?
(3)试探究:经过多少秒后,点P、Q两点间的距离为6个单位.
查看答案和解析>>
科目:初中数学 来源: 题型:
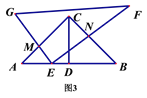
【题目】在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D是AB边上的中点,Rt△EFG的直角顶点E在AB边上移动.
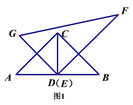
(1)如图1,若点D与点E重合且EG⊥AC、DF⊥BC,分别交AC、BC于点M、N,
易证EM=EN;如图2,若点D与点E重合,将△EFG绕点D旋转,则线段EM与EN的长度还相等吗?若相等请给出证明,不相等请说明理由;
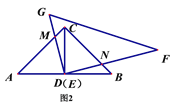
(2)将图1中的Rt△EGF绕点O顺时针旋转角度α(0<α<45). 如图2,在旋转过程中,当∠MDC=15时,连接MN,若AC=BC=2,请求出写出线段MN的长;
(3) 图3, 旋转后,若Rt△EGF的顶点E在线段AB上移动(不与点D、B重合),当AB=3AE时,线段EM与EN的数量关系是________;当AB=m·AE时,线段EM与EN的数量关系是__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
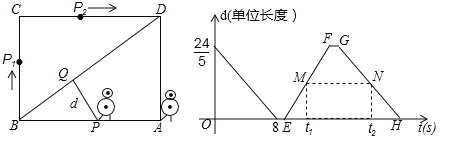
【题目】(2017江苏省苏州市)某校机器人兴趣小组在如图①所示的矩形场地上开展训练.机器人从点A出发,在矩形ABCD边上沿着A→B→C→D的方向匀速移动,到达点D时停止移动.已知机器人的速度为1个单位长度/s,移动至拐角处调整方向需要1s(即在B、C处拐弯时分别用时1s).设机器人所用时间为t(s)时,其所在位置用点P表示,P到对角线BD的距离(即垂线段 PQ的长)为d个单位长度,其中d与t的函数图象如图②所示.
(1)求AB、BC的长;
(2)如图②,点M、N分别在线段EF、GH上,线段MN平行于横轴,M、N的横坐标分别为t1、t2.设机器人用了t1(s)到达点P1处,用了t2(s)到达点P2处(见图①).若CP1+CP2=7,求t1、t2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1,![]() ),则点C的坐标为( )
),则点C的坐标为( )

A. (![]() ,-1)B. (-1,
,-1)B. (-1,![]() )C. (
)C. (![]() ,1)D. (-
,1)D. (-![]() ,1)
,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
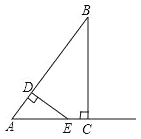
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,动点D从点A出发以每秒3个单位的速度运动至点B,过点D作DE⊥AB交射线AC于点E.设点D的运动时间为t秒(t>0).
(1)线段AE的长为 .(用含t的代数式表示)
(2)若△ADE与△ACB的面积比为1:4时,求t的值.
(3)设△ADE与△ACB重叠部分图形的周长为L,求L与t之间的函数关系式.
(4)当直线DE把△ACB分成的两部分图形中有一个是轴对称图形时,直接写出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在航线l的两侧分别有观测点A和B,点B到航线l的距离BD为4km,点A位于点B北偏西60°方向且与B相距20km处.现有一艘轮船从位于点A南偏东74°方向的C处,沿该航线自东向西航行至观测点A的正南方向E处.求这艘轮船的航行路程CE的长度.(结果精确到0.1km)(参考数据:![]() ≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)
≈1.73,sin74°≈0.96,cos74°≈0.28,tan74°≈3.49)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC⊥AB,E为⊙O上的一点,AC=EC,延长CE交AB的延长线于点D.

(1)求证:CE为⊙O的切线;
(2)若OF⊥AE,OF=1,∠OAF=30°,求图中阴影部分的面积.(结果保留π)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com