
【题目】在等腰直角三角形ABC中,∠ACB=90°,AC=BC,D是AB边上的中点,Rt△EFG的直角顶点E在AB边上移动.
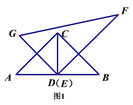
(1)如图1,若点D与点E重合且EG⊥AC、DF⊥BC,分别交AC、BC于点M、N,
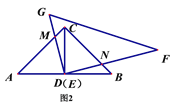
易证EM=EN;如图2,若点D与点E重合,将△EFG绕点D旋转,则线段EM与EN的长度还相等吗?若相等请给出证明,不相等请说明理由;
(2)将图1中的Rt△EGF绕点O顺时针旋转角度α(0<α<45). 如图2,在旋转过程中,当∠MDC=15时,连接MN,若AC=BC=2,请求出写出线段MN的长;
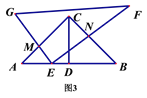
(3) 图3, 旋转后,若Rt△EGF的顶点E在线段AB上移动(不与点D、B重合),当AB=3AE时,线段EM与EN的数量关系是________;当AB=m·AE时,线段EM与EN的数量关系是__________.
【答案】 NE=2ME EN=(m-1)ME
【解析】分析:(1)易证△CDM≌△BDN,从而得出DM=DN 即EM=EN;
(2)作DP⊥AC于P,通过解直角三角形DPM得出DM=![]() ,由△MND为等腰直角三角形得出结论;
,由△MND为等腰直角三角形得出结论;
(3)过点E作EP⊥AB交AC于点P,则△AEP为等腰直角三角形,通过证明△PME∽△BNE,得到EN=2EM,由此规律可知,当AB=m·AE时,EN=(m-1)·ME
详解:(1)EM=EN;原因如下:
∵∠ACB=90° AC=BC D是AB边上的中点
∴DC=DB ∠ACD=∠B=45° ∠CDB=90°
∴∠CDF+∠FDB=90°
∵∠GDF=90°∴∠GDC+∠CDF=90°∴∠CDM=∠BDN
在△CDM和△BDN中
∠MCD=∠B,DC=DB,∠CDM=∠BDN,
∴△CDM≌△BDN ∴DM=DN 即EM=EN
(2)作DP⊥AC于P,则
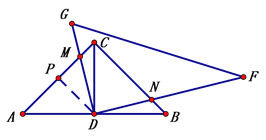
∠CDP=45° CP=DP=AP=1
∵∠CDG=15° ∴∠MDP=30°
∵cos∠MDP=![]()
∴DM=![]() , DM=DN,
, DM=DN,
∵△MND为等腰直角三角形
∴MN=![]()
(3)NE=2ME,EN=(m-1)ME
证明:如图3,过点E作EP⊥AB交AC于点P
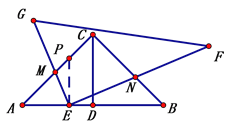
则△AEP为等腰直角三角形,∠PEB=90°
∴AE=PE ∵AB=3AE ∴BE=2AE ∴BE=2PE
又∵∠MEP+∠PEN=90°
∠PEN+∠NEB=90°
∴∠MEP=∠NEB
又∵∠MPE=∠B=45°
∴△PME∽△BNE
∴![]() ,即EN=2EM
,即EN=2EM
由此规律可知,当AB=m·AE时,EN=(m-1)·ME


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动1m.其行走路线如图所示,第1次移动到A1,第2次移动到A2,…,第n次移动到An.则△OA2A2018的面积是( )

A. 504m2 B. ![]() m2 C.
m2 C. ![]() m2 D. 1009m2
m2 D. 1009m2
查看答案和解析>>
科目:初中数学 来源: 题型:
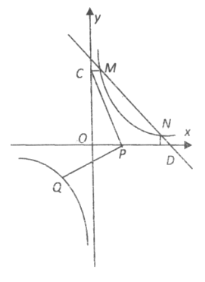
【题目】已知:如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
(1)直接写出M、N的坐标及k的值;
(2)将线段CP绕点P按逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出点Q的坐标;如果不能,请说明理由;
(3)当点P滑动时,是否存在反比例函数图象(第一象限的一支)上的点S,使得以P、S、M、N四个点为顶点的四边形是平行四边形?若存在,请直接写出所有符合题意的点S的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
方案A:按流量计费,0.1元/M;
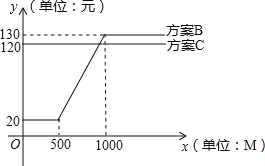
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
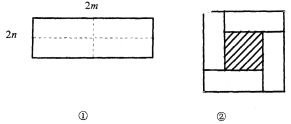
(1)你认为图②中的阴影部分的正方形的边长等于_______________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①___________________. 方法②________________.
(3)观察图②,你能写出![]() 这三个代数式之间的等量关系吗?
这三个代数式之间的等量关系吗?
(4)利用以上等量关系,解决问题:已知a+b=3,ab=-2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】发现
如图1,在有一个“凹角∠A1A2A3”n边形A1A2A3A4……An中(n为大于3的整数),∠A1A2A3=∠A1+∠A3+∠A4+∠A5+∠A6+……+∠An﹣(n﹣4)×180°.
验证
(1)如图2,在有一个“凹角∠ABC”的四边形ABCD中,证明:∠ABC=∠A+∠C+∠D.
(2)证明3,在有一个“凹角∠ABC”的六边形ABCDEF中,证明;∠ABC=∠A+∠C+∠D+∠E+∠F﹣360°.
延伸
(3)如图4,在有两个连续“凹角A1A2A3和∠A2A3A4”的四边形A1A2A3A4……An中(n为大于4的整数),∠A1A2A3+∠A2A3A4=∠A1+∠A4+∠A5+∠A6……+∠An﹣(n﹣ )×180°.

查看答案和解析>>
科目:初中数学 来源: 题型:
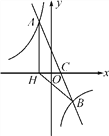
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 ![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
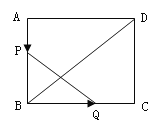
【题目】如图,已知矩形![]() ,长
,长![]() ,宽
,宽![]() ,
, ![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上运动的两点。若
上运动的两点。若![]() 自点
自点![]() 出发,以
出发,以![]() 的速度沿
的速度沿![]() 方向运动,同时,
方向运动,同时, ![]() 自点
自点![]() 出发以
出发以![]() 的速度沿
的速度沿![]() 方向运动,则经过____________秒,以
方向运动,则经过____________秒,以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似。
相似。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有4个标有1,2,3,4的小球,它们的形状、大小完全相同,小明从布袋里随机取出一个小球,记下数字为x,小红在剩下的3个小球中随机取出一个小球,记下数字为y
(1)计算由x、y确定的点(x,y)在函数y=﹣x+5的图象上的概率.
(2)小明和小红约定做一个游戏,其规则为:若x、y满足xy>6,则小明胜;若x、y满足xy<6,则小红胜,这个游戏公平吗?请说明理由;若不公平,请写出公平的游戏规则.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com