
【题目】如图,点P、Q在数轴上表示的数分别是-8、4,点P以每秒2个单位的速度运动,点Q以每秒1个单位的速度运动.设点P、Q同时出发向右运动,运动时间为t秒.

(1)若运动2秒时,则点P表示的数为_______,点P、Q之间的距离是______个单位;
(2)求经过多少秒后,点P、Q重合?
(3)试探究:经过多少秒后,点P、Q两点间的距离为6个单位.
【答案】(1)-4,10;(2)12秒;(3)6秒或18秒
【解析】
(1)根据数轴上的数向右移动加列式计算即可得解,写出出P、Q两点表示的数,计算即可;
(2)用t列出P、Q表示的数,列出等式求解即可;
(3)点P、Q同时出发向右运动,运动时间为t秒,分为两种情况讨论①未追上时,②追上且超过时,分别算出即可.
解:(1)点P表示的数是: -8+2×2=-4
点Q表示的数是: 4+2×1=6
点P、Q之间的距离是: 6-(-4)=10;
(2)∵点P、Q同时出发向右运动,运动时间为t秒,
点P、Q重合时,-8+2t=4+t, 解得:t=12 (秒)
经过12秒后,点P、Q重合;
(3)点P、Q同时出发向右运动,运动时间为t秒,
故分为两种情况讨论:
①未追上时:(4+t)-(-8+2t)= 6
解得:t= 6 (秒)
②追上且超过时:(-8+2t)—(4+t)= 6
解得:t= 18 (秒)
答:经过6秒或18秒后,点P、Q两点间的距离为6个单位.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,分别以点A和点B为圆心,以相同的长(大于![]() AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )
AB)为半径作弧,两弧相交于点M和点N,作直线MN交AB于点D,交BC于点E.若AC=3,AB=5,则DE等于( )

A. 2 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
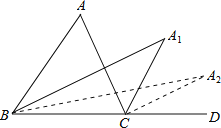
【题目】如图,在△ABC中,∠A=640,∠ABC和∠ACD的平分线交于点A1,得∠A1;∠A1BC和∠A1CD的平分线交于点A2,得∠A2;∠A2BC和∠A2CD的平分线交于点A3,则∠A5= ______ .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,一次函数![]() 的图象与反比例函数
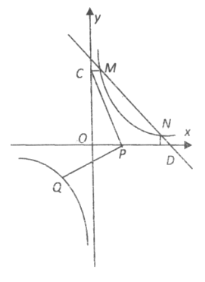
的图象与反比例函数![]() 的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
的图象交于M,N两点,过点M作MC⊥y轴于点C,且CM=1,过点N作ND⊥x轴于点D,且DN=1,已知点P是x轴(除原点O外)上一点.
(1)直接写出M、N的坐标及k的值;
(2)将线段CP绕点P按逆时针旋转90°得到线段PQ,当点P滑动时,点Q能否在反比例函数的图象上?如果能,求出点Q的坐标;如果不能,请说明理由;
(3)当点P滑动时,是否存在反比例函数图象(第一象限的一支)上的点S,使得以P、S、M、N四个点为顶点的四边形是平行四边形?若存在,请直接写出所有符合题意的点S的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设A、B、C、D为平面上任意四点,如果其中任意三点不在同一直线上,则△ABC、△ABD、△ACD、△BCD中至少存在一个三角形的某个内角满足( )
A.不超过 15°B.不超过 30°C.不超过 45°D.以上都不对
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
方案A:按流量计费,0.1元/M;
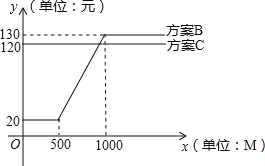
方案B:20元流量套餐包月,包含500M流量,如果超过500M,超过部分另外计费(见图象),如果用到1000M时,超过1000M的流量不再收费;
方案C:120元包月,无限制使用.
用x表示每月上网流量(单位:M),y表示每月的流量费用(单位:元),方案B和方案C对应的y关于x的函数图象如图所示,请解决以下问题:
(1)写出方案A的函数解析式,并在图中画出其图象;
(2)直接写出方案B的函数解析式;
(3)若甲乙两人每月使用流量分别在300—600M,800—1200M之间,请你分别给出甲乙二人经济合理的选择方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.
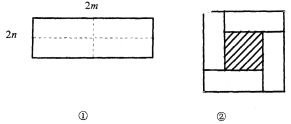
(1)你认为图②中的阴影部分的正方形的边长等于_______________.
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法①___________________. 方法②________________.
(3)观察图②,你能写出![]() 这三个代数式之间的等量关系吗?
这三个代数式之间的等量关系吗?
(4)利用以上等量关系,解决问题:已知a+b=3,ab=-2,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
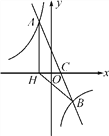
【题目】如图,在平面直角坐标系中,一次函数y=ax+b(a≠0)的图象与反比例函数y=![]() (k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4
(k≠0)的图象交于A,B两点,与x轴交于点C,过点A作AH⊥x轴于点H,点O是线段CH的中点,AC=4 ![]() ,cos∠ACH=
,cos∠ACH=![]() ,点B的坐标为(4,n).
,点B的坐标为(4,n).
(1)求该反比例函数和一次函数的解析式;
(2)求△BCH的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是∠AOB内任意一点,OP=5cm,点M和点N分别是射线OA和射线OB上的动点,△PMN周长的最小值是5cm,则∠AOB的度数是( )

A. 25° B. 30° C. 35° D. 40°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com