
 ��ͼ����ƽ���ı���ABCD�У��Խ���BD=12cm��AC=16cm��AC��BD�ཻ�ڵ�O����E��F��AC�������㣬�ֱ��A��C��������ͬ���ٶ���C��A�˶������ٶ�Ϊ0.5cm/s��
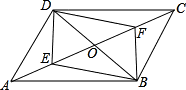
��ͼ����ƽ���ı���ABCD�У��Խ���BD=12cm��AC=16cm��AC��BD�ཻ�ڵ�O����E��F��AC�������㣬�ֱ��A��C��������ͬ���ٶ���C��A�˶������ٶ�Ϊ0.5cm/s������ ��1��������֪��AE=CF���Ƴ�OE=OF������ƽ���ı��ε����ʵó�OD=OB������ƽ���ı��ε��ж��Ƴ����ɣ�
��2�����ݾ��ε����ʵó�EF=BD=12���ó�����16-0.5t-0.5t=12��������ɣ���E��F����λ��ʱ�ó�����0.5t-12+0.5t=16��������ɣ�
��� �⣺��1����E��F��AC�������㣬�ֱ��A��C��������ͬ���ٶ���C��A�˶���
��AE=CF��
���ı���ABCD��ƽ���ı��Σ�
��OD=OB��OA=OC��
��OA-AE=OC-CF��
��OE=OF��
���ı���DEBF��ƽ���ı��Σ�
��2����E��F��AC���˶������У���D��E��B��FΪ������ı�����Ϊ���Σ��������£�
�����������
�١��ı���DEBF�Ǿ��Σ�
��BD=EF=12cm��
��AE=CF=0.5tcm��
��16-0.5t-0.5t=12��
��ã�t=4��
�ڵ�E��Fλ���ϣ�F��Eλ����ʱ��AE=AF=0.5tcm��
��0.5t-12+0.5t=16��
��ã�t=28��
�����˶�ʱ��t=4s��28sʱ����D��E��B��FΪ������ı����Ǿ���
���� ���⿼���˾��ε����ʺ��ж���ƽ���ı��ε����ʺ��ж���֪ʶ�㣬��Ҫ����ѧ���������ʽ��������ͼ������������Ŀ�ȽϺã�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��ʾ����ƽ��ֱ������ϵ�У�������y=-$\frac{4}{3}{x}^{2}+bx+c$��x�ύ��A��B���㣬��y�ύ��C�㣬����B��3��0����C��0��4������A��x��ĸ������ϣ�
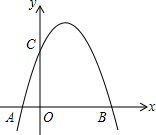
��ͼ��ʾ����ƽ��ֱ������ϵ�У�������y=-$\frac{4}{3}{x}^{2}+bx+c$��x�ύ��A��B���㣬��y�ύ��C�㣬����B��3��0����C��0��4������A��x��ĸ������ϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����10��10�������������У�ÿ��С�����εı߳�Ϊ1����λ���ȣ���ABC�Ķ��㶼������������ĸ���ϣ���ͨ������ƽ�ƣ��������߷��������»�����ƽ�ƣ���õ���A��B��C�䣬��C�Ķ�Ӧ����ֱ���ϵĸ��C�䣮
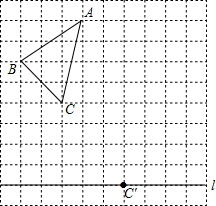
��ͼ����10��10�������������У�ÿ��С�����εı߳�Ϊ1����λ���ȣ���ABC�Ķ��㶼������������ĸ���ϣ���ͨ������ƽ�ƣ��������߷��������»�����ƽ�ƣ���õ���A��B��C�䣬��C�Ķ�Ӧ����ֱ���ϵĸ��C�䣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 3 | C�� | 4 | D�� | 5 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
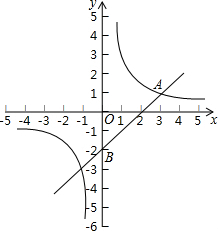 ��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڵ�A��3��1�����ҹ���B��0��-2����
��ͼ����ƽ��ֱ������ϵ�У�һ�κ���y=kx+b�뷴��������y=$\frac{m}{x}$��m��0����ͼ���ڵ�A��3��1�����ҹ���B��0��-2�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
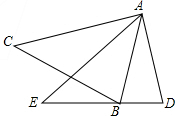 ��ͼ���ڡ�ADE�У���CAE=��BAD��AC=AE��
��ͼ���ڡ�ADE�У���CAE=��BAD��AC=AE���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com