0+-1-3$\sqrt{\frac{1}{3}}$+|-$\sqrt{3}$| 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

8．（6-π）⁰+（-$\frac{1}{5}$）^-1-3$\sqrt{\frac{1}{3}}$+|-$\sqrt{3}$|

分析原式利用零指数幂、负整数指数幂法则，二次根式性质，以及绝对值的代数意义化简，计算即可得到结果．

解答解：原式=1-5-3×$\frac{\sqrt{3}}{3}$+$\sqrt{3}$
=-4．

点评此题考查了实数的运算，熟练掌握运算法则是解本题的关键．

练习册系列答案

中考考点分类突破卷系列答案

中考先锋中考总复习系列答案

新题型全程检测期末冲刺100分系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：填空题

1．如果最简二次根式$\sqrt{3a-8}$与$\sqrt{7}$的被开方数相同，则a=5．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

20．

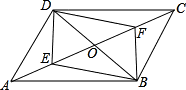如图，在平行四边形ABCD中，对角线BD=12cm，AC=16cm，AC，BD相交于点O，若E，F是AC上两动点，分别从A，C两点以相同的速度向C、A运动，其速度为0.5cm/s．
（1）证明：当E在AO上运动，F在CO上运动，且E与F不重合时，四边形DEBF是平行四边形；
（2）点E，F在AC上运动过程中，以D、E、B、F为顶点的四边形是否可能为矩形？如能，求出此时的运动时间t的值；如不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

17．计算：
（1）$\frac{{a}^{2}-4}{8{a}^{2}b}•\frac{12ab}{3a-6}$
（2）$\frac{2}{x-2}-\frac{8}{{x}^{2}-4}$．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

3．

在一年一度的国家学生体质侧试中，金星中学对全饺2000名男生的1000m测试成绩进行了抽查，学校从初三年级抽取了一部分男生的成绩，并制作成统计表，绘制成频数直方图．

序号	范围（单位：秒）	频数	频率
1	170＜x≤200	5	0.1
2	200＜x≤230	13	a
3	230＜x≤260	15	0.3
4	260＜x≤290	c	d
5	290＜x≤320	5	0.1
6	320＜x≤350	2	0.04
7	350＜x≤380	2	0.04
合计		b	1.00

（1）在这个问题中，总体是什么？
（2）直接写出a，b，c，d的值．
（3）补全频数直方图．
（4）初中毕业生体能测试项目成绩评定标准是男生1000m不超过4′20″（即260秒）为合格，你能估计出该校初中男生的1000m的合格人数吗？如果能，请求出合格的人数；如果不能，请说明理由．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

13．

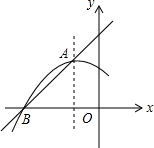如图是抛物线y₁=ax²+bx+c（a≠0）的图象的一部分，抛物线的顶点A的坐标为（-1，2），与x轴的一个交点B的坐标为（-3，0），直线y₂=mx+n与抛物线交于A、B两点．下列结论：①2a-b=0；②abc＜0；③a+b+c=0；④方程ax²+bx+c=5没有实数根；⑤当y₁＜y₂时，x＞-1．其中正确的是（　　）

A．

①③④

B．

①③④⑤

C．

①③⑤

D．

②③④⑤

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

20．

如图是一把剪刀，若∠1与∠2互为余角，则∠1=45°．