
【题目】如图所示,正比例函数y=![]() x的图象与反比例函数y=
x的图象与反比例函数y=![]() (k≠0)在第一象限的图象交于点
(k≠0)在第一象限的图象交于点![]() ,过点A作X轴的垂线,垂足为M,已知△AOM的面积为1.
,过点A作X轴的垂线,垂足为M,已知△AOM的面积为1.
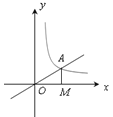
(1)求反比例函数的解析式;
(2)如果点![]() 为反比例函数在第一象限图象上的点(点
为反比例函数在第一象限图象上的点(点![]() 与点
与点![]() 不重合),且点
不重合),且点![]() 的横坐标为1,在
的横坐标为1,在![]() 轴上求一点
轴上求一点![]() ,使
,使![]() 最小.
最小.
【答案】(1)y=![]() ;(2)P点坐标为(
;(2)P点坐标为(![]() ,0)
,0)
【解析】
试题分析:(1) 设A点的坐标为(a,b),于是ab=k .又由△AOM的面积为1.得到![]() ab=1 ,∴
ab=1 ,∴![]() k=1 .进而求得k值,确定反比例函数解析式;(2)由两个函数解析式求得交点A的坐标,又由B点的横坐标为1,及反比例函数解析式求得B点坐标,作A点关于x轴的对称点C,连接BC,交x轴于一点,即为符合要求的P点,然后由B,C两点坐标求出直线BC的解析式,即可求出P点坐标.
k=1 .进而求得k值,确定反比例函数解析式;(2)由两个函数解析式求得交点A的坐标,又由B点的横坐标为1,及反比例函数解析式求得B点坐标,作A点关于x轴的对称点C,连接BC,交x轴于一点,即为符合要求的P点,然后由B,C两点坐标求出直线BC的解析式,即可求出P点坐标.
试题解析:(1)根据题意可设A点的坐标为(a,b),则b=![]() .∴ab=k .
.∴ab=k .
∵△AOM的面积为1.
∴![]() ab=1 ,
ab=1 ,
∴![]() k=1 .
k=1 .
∴ k=2.
∴ 反比例函数的解析式为y=![]() ;
;
(2) 由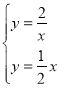 得
得![]() 或
或![]() ,
,
∵A在第一象限,
∴ A为(2,1),设A点关于x轴的对称点为C,
则C点的坐标为(2,-1)如要在x轴上求一点P,使PA+PB最小.
则P点应为BC和x轴的交点,
如图所示.设直线BC的解析式为y=mx+n.
∵ B为(1,2),
∴![]() ,解得:
,解得:![]() ,
,
∴ BC的解析式为y=-3x+5.
当y=0时,x=![]() .
.
∴ P点坐标为(![]() ,0)
,0)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】我们学校教室里的饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温(℃)与开机后用时(min)成反比例关系.直至水温降至30℃,饮水机关机.饮水机关机后即刻自动开机,重复上述自动程序.若在水温为30℃时,接通电源后,水温y(℃)和时间(min)的关系如图,为了在上午第一节下课时(8:30)能喝到不超过50℃的水,则接通电源的时间可以是当天上午的( )
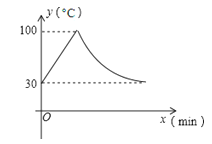
A.7:00 B.7:05 C.7:10 D.7:15
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次考试中,某班级的数学成绩统计图如下.下列说法错误的是( )
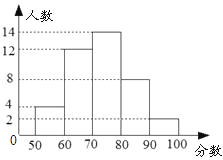
A.得分在70~80分之间的人数最多
B.该班的总人数为40
C.得分在90~100分之间的人数最少
D.及格(≥60分)人数是26
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组![]() ,其中﹣3≤a≤1,给出下列命题:
,其中﹣3≤a≤1,给出下列命题:
①![]() 是方程组的解;
是方程组的解;
②当a=﹣2时,x,y的值互为相反数;
③当a=1时,方程组的解也是方程x+y=4﹣a的解;
④若x≤1,则1≤y≤4.
其中正确命题的序号是 .(把所有正确命题的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个运算流程.

(1)分别计算:当x=150时,输出值为 ,当x=27时,输出值为 ;
(2)若需要经过两次运算,才能运算出y,求x的取值范围;
(3)请给出一个x的值,使之无论运算多少次都不能输出,并请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,BC=6cm,射线AG∥BC,点E从点A出发沿射线AG以1cm/s的速度运动,点F从点B出发沿射线BC以2cm/s的速度运动.如果点E、F同时出发,设运动时间为t(s),当t= s时,以A、C、E、F为顶点四边形是平行四边形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com