
【题目】解方程(组)
(1) 5x3 40 (2)4 x 12 9
(3)![]() (4 )
(4 ) ![]()
【答案】(1)x=-2;(2)x1=![]() 或x2=
或x2=![]() ;(3)x=2,y=8;(4)x=2, y=-1.
;(3)x=2,y=8;(4)x=2, y=-1.
【解析】
(1)先变形为x3=-8,再直接开立方解方程;(2)先变形为x 12=![]() ,再利用直接开平方法解方程;(3)根据二元一次方程的性质解方程组即可;(4)根据二元一次方程的性质解方程组即可.
,再利用直接开平方法解方程;(3)根据二元一次方程的性质解方程组即可;(4)根据二元一次方程的性质解方程组即可.
(1)5x3 40,
x3=-8,
x=-2;
(2)4 x 12 9,
x 12=![]() ,
,
x 1=±![]() ,
,
x=1±![]() ;
;
x1=![]() 或x2=
或x2=![]()
(3)![]() ,
,
根据②得x=10-y,
代入①得2(10-y)-y=-4,
20-2y-y=-4,
3y=24,则y=8,
故x=10-8=2;
(4)![]() ,
,
根据②得y=3-2x,
代入①得3x-5(3-2x)=11,
3x-15+10x=11,
13x=26,
x=2,则y=-1.


科目:初中数学 来源: 题型:
【题目】用配方法解下列方程时,配方正确的是( )
A.方程x2﹣6x﹣5=0,可化为(x﹣3)2=4
B.方程y2﹣2y﹣2015=0,可化为(y﹣1)2=2015
C.方程a2+8a+9=0,可化为(a+4)2=25
D.方程2x2﹣6x﹣7=0,可化为 ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() ABCD中,F是AD的中点,延长BC到点E,使CE=
ABCD中,F是AD的中点,延长BC到点E,使CE=![]() BC,连结DE,CF。
BC,连结DE,CF。

(1)求证:四边形CEDF是平行四边形;
(2)若AB=4,AD=6,∠B=60°,求DE的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中(AD>AB),点E是BC上一点,且DE=DA,AF⊥DE,垂足为点F,在下列结论中,不一定正确的是( ) 
A.△AFD≌△DCE
B.AF= ![]() AD
AD
C.AB=AF
D.BE=AD﹣DF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC沿DE、HG、EF分别翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( ).

A. 78° B. 102° C. 112° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠BAC=60°,AD=AE,BE、CD交于点F,且∠DFE=120°.在BE的延长线上截取ET=DC,连接AT.
(1)求证:∠ADC=∠AET;
(2)求证:AT=AC;
(3)设BC边上的中线AP与BE交于Q.求证:∠QAB=∠QBA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.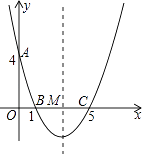
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com