
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.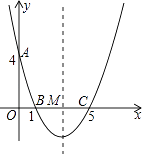
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】
(1)
解:根据已知条件可设抛物线的解析式为y=a(x﹣1)(x﹣5),
把点A(0,4)代入上式得:a= ![]() ,
,
∴y= ![]() (x﹣1)(x﹣5)=
(x﹣1)(x﹣5)= ![]() x2﹣
x2﹣ ![]() x+4=
x+4= ![]() (x﹣3)2﹣
(x﹣3)2﹣ ![]() ,
,
∴抛物线的对称轴是:x=3
(2)
解:P点坐标为(3, ![]() ).
).
理由如下:
∵点A(0,4),抛物线的对称轴是x=3,
∴点A关于对称轴的对称点A′的坐标为(6,4)
如图1,连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小.
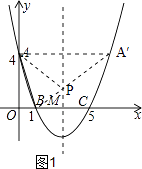
设直线BA′的解析式为y=kx+b,
把A′(6,4),B(1,0)代入得 ![]() ,
,
解得 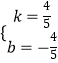 ,
,
∴y= ![]() x﹣
x﹣ ![]() ,
,
∵点P的横坐标为3,
∴y= ![]() ×3﹣
×3﹣ ![]() =
= ![]() ,
,
∴P(3, ![]() ).
).
(3)
解:在直线AC的下方的抛物线上存在点N,使△NAC面积最大.
设N点的横坐标为t,此时点N(t, ![]() t2﹣
t2﹣ ![]() t+4)(0<t<5),
t+4)(0<t<5),
如图2,过点N作NG∥y轴交AC于G;作AD⊥NG于D,
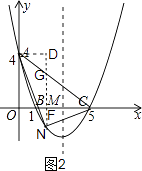
由点A(0,4)和点C(5,0)可求出直线AC的解析式为:y=﹣ ![]() x+4,
x+4,
把x=t代入得:y=﹣ ![]() t+4,则G(t,﹣
t+4,则G(t,﹣ ![]() t+4),
t+4),
此时:NG=﹣ ![]() t+4﹣(
t+4﹣( ![]() t2﹣
t2﹣ ![]() t+4)=﹣
t+4)=﹣ ![]() t2+4t,
t2+4t,
∵AD+CF=CO=5,
∴S△ACN=S△ANG+S△CGN= ![]() AD×NG+
AD×NG+ ![]() NG×CF=
NG×CF= ![]() NGOC=
NGOC= ![]() ×(﹣
×(﹣ ![]() t2+4t)×5=﹣2t2+10t=﹣2(t﹣
t2+4t)×5=﹣2t2+10t=﹣2(t﹣ ![]() )2+
)2+ ![]() ,
,
∴当t= ![]() 时,△CAN面积的最大值为
时,△CAN面积的最大值为 ![]() ,
,
由t= ![]() ,得:y=
,得:y= ![]() t2﹣
t2﹣ ![]() t+4=﹣3,
t+4=﹣3,
∴N( ![]() ,﹣3)
,﹣3)
【解析】(1)抛物线经过点A(0,4),B(1,0),C(5,0),可利用两点式法设抛物线的解析式为y=a(x﹣1)(x﹣5),代入A(0,4)即可求得函数的解析式,则可求得抛物线的对称轴;(2)点A关于对称轴的对称点A′的坐标为(6,4),连接BA′交对称轴于点P,连接AP,此时△PAB的周长最小,可求出直线BA′的解析式,即可得出点P的坐标.(3)在直线AC的下方的抛物线上存在点N,使△NAC面积最大.设N点的横坐标为t,此时点N(t, ![]() t2﹣
t2﹣ ![]() t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.
t+4)(0<t<5),再求得直线AC的解析式,即可求得NG的长与△ACN的面积,由二次函数最大值的问题即可求得答案.


科目:初中数学 来源: 题型:
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 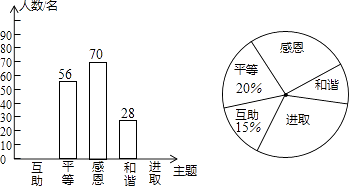
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
查看答案和解析>>
科目:初中数学 来源: 题型:
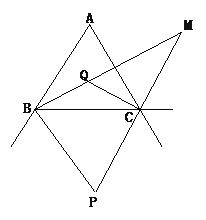
【题目】如图,△ABC的两外角平分线交于点P,易证∠P=90°-![]() ∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+
∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+![]() ∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某办公楼AB的后面有一建筑物CD,当光线与地面的夹角是22°时,办公楼在建筑物的墙上留下高2米的影子CE,而当光线与地面夹角是45°时,办公楼顶A在地面上的影子F与墙角C有25米的距离(B,F,C在一条直线上). 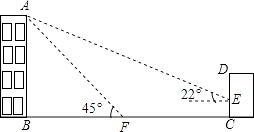
(参考数据:sin22°≈ ![]() ,cos22°
,cos22° ![]() ,tan22
,tan22 ![]() )
)
(1)求办公楼AB的高度;
(2)若要在A,E之间挂一些彩旗,请你求出A,E之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠A=150°.第一步:在△ABC上方确定一点A1,使∠A1BA=∠ABC,∠A1CA=∠ACB,如图1.第二步:在△A1BC上方确定一点A2,使∠A2BA1=∠A1BA,∠A2CA1=∠A1CA,如图2.照此下去,至多能进行( )步.
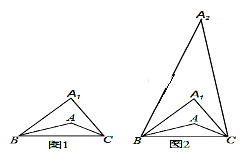
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE,动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P的运动时间为t秒,当t的值为__________秒时.△ABP和△DCE全等.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com