
【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的5个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题: 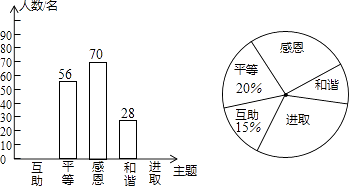
(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这5个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
【答案】
(1)解:56÷20%=280(名),
答:这次调查的学生共有280名
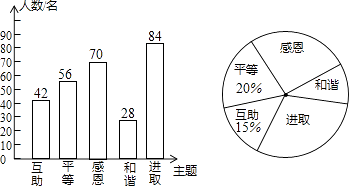
(2)解:280×15%=42(名),280﹣42﹣56﹣28﹣70=84(名),
补全条形统计图,如图所示,
根据题意得:84÷280=30%,360°×30%=108°,
答:“进取”所对应的圆心角是108°
(3)解:由(2)中调查结果知:学生关注最多的两个主题为“进取”和“感恩”用列表法为:
A | B | C | D | E | |
A | (A,B) | (A,C) | (A,D) | (A,E) | |
B | (B,A) | (B,C) | (B,D) | (B,E) | |
C | (C,A) | (C,B) | (C,D) | (C,E) | |
D | (D,A) | (D,B) | (D,C) | (D,E) | |
E | (E,A) | (E,B) | (E,C) | (E,D) |
用树状图为:

共20种情况,恰好选到“C”和“E”有2种,
∴恰好选到“进取”和“感恩”两个主题的概率是 ![]()
【解析】(1)根据“平等”的人数除以占的百分比得到调查的学生总数即可;(2)求出“互助”与“进取”的学生数,补全条形统计图,求出“进取”占的圆心角度数即可;(3)列表或画树状图得出所有等可能的情况数,找出恰好选到“C”与“E”的情况数,即可求出所求的概率.


科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将△ABC沿DE、HG、EF分别翻折,三个顶点均落在点O处,且EA与EB重合于线段EO,若∠DOH=78°,则∠FOG的度数为( ).

A. 78° B. 102° C. 112° D. 120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图所示,在△ABC中,∠BAC=60°,AD=AE,BE、CD交于点F,且∠DFE=120°.在BE的延长线上截取ET=DC,连接AT.
(1)求证:∠ADC=∠AET;
(2)求证:AT=AC;
(3)设BC边上的中线AP与BE交于Q.求证:∠QAB=∠QBA.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=12,点E在边CD上,且BG=CG,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②∠EAG=450;③CE=2DE;④AG∥CF;⑤S△FGC=![]() .其中正确结论的个数是( )
.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠ABC=70°,以B为圆心,任意长为半径画弧交AB,BC于点E,F,再分别以点E,F为圆心、以大于![]() EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.
EF长为半径画弧,两弧交于点P,作射线BP交AC于点D,则∠BDC为( )度.

A. 65 B. 75 C. 80 D. 85
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.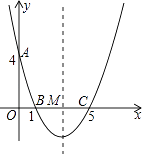
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com