
【题目】如图所示,一次函数y=x+3与x轴、y轴分别交于点A、B,将直线AB向下平移与反比例函数![]() (x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=
(x>0)交于点C、D,连接BC交x轴于点E,连接AC,已知BE=3CE,且S△ACE=![]() .
.
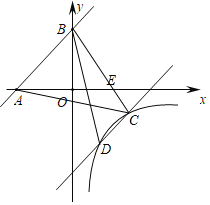
(1)求直线BC和反比例函数解析式;(2)连接BD,求△BCD的面积.
【答案】(1)![]() ,
,![]() ;(2)S△BCD=
;(2)S△BCD=![]() .
.
【解析】
(1)作CF⊥x轴于F,根据BE=3CE,且S△ACE=![]() 求得S△ABE=
求得S△ABE=![]() ,根据三角形面积求得AE,从而求得OE和CF,由三角形相似求得EF,得到C点的坐标,即可根据勾股定理求得BC,根据反比例函数图象上点的坐标特征求得反比例函数的解析式;
,根据三角形面积求得AE,从而求得OE和CF,由三角形相似求得EF,得到C点的坐标,即可根据勾股定理求得BC,根据反比例函数图象上点的坐标特征求得反比例函数的解析式;
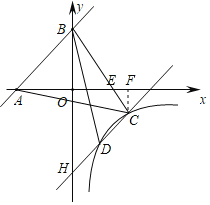
(2)设直线CD的解析式为y=x+b,令直线CD交y轴于H,根据待定系数法求得解析式,从而求得H点的坐标,联立方程求得D点的坐标,然后根据S△BCD=S△BCH﹣S△BDH求得即可.
(1)作CF⊥x轴于F,
由直线y=x+3可知,A(﹣3,0),B(0,3),
∵BE=3CE,且S△ACE=![]() ,
,
∴S△ABE=![]() ,
,
∴![]() AEOB=
AEOB=![]() ,即
,即![]() AE3=
AE3=![]() ,
,
∴AE=![]() ,
,
∴OE=![]() ,
,
∵S△ACE=![]() AECF=
AECF=![]() ,
,
∴CF=1,
∵CF∥OB,
∴△ECF∽△EBO,
∴![]() ,即
,即![]() =
=![]() ,
,
∴EF=![]() ,
,
∴OF=OE+DF
∴C(2,﹣1),
∴BC=![]() ,
,
∵反比例函数y=![]() (x>0)经过点C,
(x>0)经过点C,
∴m=2×(﹣1)=﹣2,
∴反比例函数解析式为y=﹣![]() ;
;
(2)∵将直线AB向下平移与反比例函数y=![]() (x>0)交于点C、D,
(x>0)交于点C、D,
∴设直线CD的解析式为y=x+b,令直线CD交y轴于H,
把C(2,﹣1)代入得,﹣1=2+b,
∴b=﹣3,
∴直线CD的解析式为y=x﹣3,
∴H(0,﹣3),
解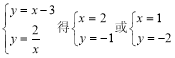 ,
,
∴D(1,﹣2),
∴S△BCD=S△BCH﹣S△BDH=![]() ×3×2﹣
×3×2﹣![]() ×3×1=
×3×1=![]() .
.


科目:初中数学 来源: 题型:
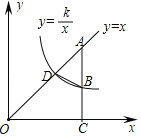
【题目】如图,直线y=x与反比例函数y=![]() (x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=
(x>0)的图象相交于点D,点A为直线y=x上一点,过点A作AC⊥x轴于点C,交反比例函数y=![]() (x>0)的图象于点B,连接BD.
(x>0)的图象于点B,连接BD.
(1)若点B的坐标为(8,2),则k= ,点D的坐标为 ;
(2)若AB=2BC,且△OAC的面积为18,求k的值及△ABD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)数学理解:如图①,![]() 是等腰直角三角形,过斜边
是等腰直角三角形,过斜边![]() 的中点
的中点![]() 作正方形
作正方形![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,求证:
,求证:![]() ;
;
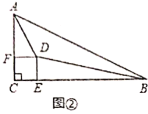
(2)问题解决:如图②,在任意直角![]() 内,找一点
内,找一点![]() ,过点
,过点![]() 作正方形
作正方形![]() ,分别交
,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,若
,若![]() ,求
,求![]() 的度数;
的度数;
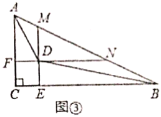
(3)联系拓广;如图③,在(2)的条件下,分别延长![]() ,
,![]() ,交
,交![]() 于点
于点![]() ,
,![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.
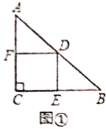
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知甲、乙两地相距![]() 车和
车和![]() 车分别从甲地和乙地同时出发,相向而行,沿同一 条公路驶往乙地和甲地
车分别从甲地和乙地同时出发,相向而行,沿同一 条公路驶往乙地和甲地![]() 后,
后,![]() 车因临时需要,返回到这条公路上的丙地取物,然后又立即赶往乙地,结果比
车因临时需要,返回到这条公路上的丙地取物,然后又立即赶往乙地,结果比![]() 车晚
车晚![]() 到达目的地.两车的速度始终保持不变,如图是
到达目的地.两车的速度始终保持不变,如图是![]() 两车距各自出 发地的路程
两车距各自出 发地的路程![]() (单位:
(单位:![]() ),
),![]() (单位:
(单位:![]() )与
)与![]() 车出发时间
车出发时间![]() (单位:
(单位:![]() )的函数图象,请结合图象信息解答下列问题:
)的函数图象,请结合图象信息解答下列问题:

(1)A车的速度为 ![]() 车的速度为
车的速度为
(2)求甲、丙两地的距离;
(3)求![]() 车出发多长时间,两车相距
车出发多长时间,两车相距![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
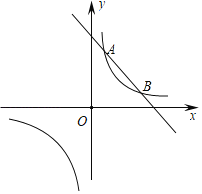
【题目】已知一次函数y=﹣x+m的图象与反比例函数![]() 的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
的图象交于A、B两(点A在点B的左侧),点P为x轴上一动点,当有且只有一个点P,使得∠APB=90°,则m的值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?
(2)今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=2![]() ,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )
,BC=10,E、F分别在边BC,AD上,BE=DF.将△ABE,△CDF分别沿着AE,CF翻折后得到△AGE,△CHF.若AG、CH分别平分∠EAD、∠FCB,则GH长为( )

A.3B.4C.5D.7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在学习概率的课堂上,老师提出问题:只有一张电影票,小明和小刚想通过抽取扑克牌的游戏来决定谁去看电影,请你设计一个对小明和小刚都公平的方案.
甲同学的方案:将红桃2、3、4、5四张牌背面向上,小明先抽一张,小刚从剩下的三张牌中抽一张,若两张牌上的数字之和是奇数,则小明看电影,否则小刚看电影.
(1)甲同学的方案公平吗?请用列表或画树状图的方法说明;
(2)乙同学将甲的方案修改为只用红桃3、4、5三张牌,小明先抽一张,记录后放回,小刚再从3张中随机抽一张,若两张牌上的数字之积是奇数,则小明看电影,否则小刚看电影,乙的方案公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
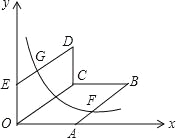
【题目】如图,0为原点,A(4,0),E(0,3),四边形OABC,四边形OCDE都为平行四边形,OC=5,函数y=![]() (x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
(x>0)的图象经过AB的中点F和DE的中点G,则k的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com