
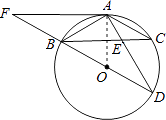
【题目】如图,BD为⊙O的直径,AB=AC,AD交BC于点E,AE=2,ED=4, 
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
【答案】
(1))证明:∵AB=AC,
∴∠ABC=∠C(等边对等角),
∵∠C=∠D(同弧所对的圆周角相等),
∴∠ABC=∠D(等量代换),
又∵∠BAE=∠DAB,
∴△ABE∽△ADB,
(2)解:∵△ABE∽△ADB,
∴ ![]() ,
,
∴AB2=ADAE=(AE+ED)AE=(2+4)×2=12,
∴AB=2 ![]() .
.
(3)解:直线FA与⊙O相切,理由如下:
连接OA,∵BD为⊙O的直径,
∴∠BAD=90°,
∴ ![]() =4
=4 ![]()
BF=BO= ![]() ,
,
∵AB=2 ![]() ,
,
∴BF=BO=AB,
∴∠OAF=90°,
∴OA⊥AF,
∵AO是圆的半径,
∴直线FA与⊙O相切.
【解析】(1)根据AB=AC,可得∠ABC=∠C,利用等量代换可得∠ABC=∠D然后即可证明△ABE∽△ADB.(2)根据△ABE∽△ADB,利用其对应边成比例,将已知数值代入即可求得AB的长.(3)连接OA,根据BD为⊙O的直径可得∠BAD=90°,利用勾股定理求得BD,然后再求证∠OAF=90°即可.
【考点精析】本题主要考查了勾股定理的概念和圆周角定理的相关知识点,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.


科目:初中数学 来源: 题型:
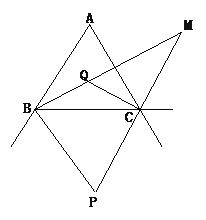
【题目】如图,△ABC的两外角平分线交于点P,易证∠P=90°-![]() ∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+
∠A;△ABC的两内角的平分线交于点Q,易证∠BQC=90°+![]() ∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
∠A;那么△ABC的内角平分线BM与外角平分CM的夹角∠M=_____∠A.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD内接于⊙O,点E在对角线AC上,EC=BC=DC. 
(1)若∠CBD=39°,求∠BAD的度数;
(2)求证:∠1=∠2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= ![]() 的图象如图,以下结论:
的图象如图,以下结论:
①m<0;
②在每个分支上y随x的增大而增大;
③若点A(﹣1,a)、点B(2,b)在图象上,则a<b;
④若点P(x,y)在图象上,则点P1(﹣x,﹣y)也在图象上.
其中正确的个数是( )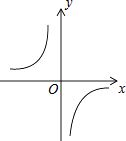
A.4个
B.3个
C.2个
D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为践行党的群众路线,六盘水市教育局开展了大量的教育教学实践活动,如图是其中一次“测量旗杆高度”的活动场景抽象出的平面几何图形.
活动中测得的数据如下:
①小明的身高DC=1.5m
②小明的影长CE=1.7cm
③小明的脚到旗杆底部的距离BC=9cm
④旗杆的影长BF=7.6m
⑤从D点看A点的仰角为30°
请选择你需要的数据,求出旗杆的高度.(计算结果保留到0.1,参考数据 ![]() ≈1.414.
≈1.414. ![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在正方形ABCD的边CD上,把△ADE绕点A顺时针旋转90°至△ABF位置,如果AB= ![]() ,∠EAD=30°,那么点E与点F之间的距离等于 .
,∠EAD=30°,那么点E与点F之间的距离等于 . 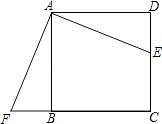
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批单价为20元的商品,若每件按24元的价格销售时,每天能卖出36件;若每件按29元的价格销售时,每天能卖出21件.假定每天销售件数y(件)与销售价格x(元/件)满足一个以x为自变量的一次函数.
(1)求y与x满足的函数关系式(不要求写出x的取值范围);
(2)在不积压且不考虑其他因素的情况下,销售价格定为多少元时,才能使每天获得的利润P最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com