
【题目】已知A、B两地相距4km,上午8:00时,亮亮从A地步行到B地,8:20时芳芳从B地出发骑自行车到A地,亮亮和芳芳两人离A地的距离S(km)与亮亮所用时间t(min)之间的函数关系如图所示,芳芳到达A地时间为( )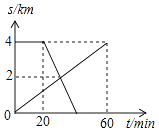
A.8:30
B.8:35
C.8:40
D.8:45
【答案】C
【解析】解:由题意可知:
设亮亮S与t的函数关系式为:S=mt(0≤t≤60),
把t=60,S=4代入S=mt,
∴4=60m,
∴m= ![]() ,
,
∴S= ![]() t,
t,
当S=2时,
此时t=30,
设芳芳S与t的函数关系式为:S=at+b(t≥20),
把t=30,S=2和t=20,S=4代入S=at+b,
![]() ,
,
解得: 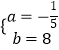 ,
,
∴S=﹣ ![]() t+8,
t+8,
令S=0代入S=﹣ ![]() t+8,
t+8,
∴t=40,
故芳芳到达A地的时间为8点40分
所以答案是:C
【考点精析】本题主要考查了函数的图象的相关知识点,需要掌握函数的图像是由直角坐标系中的一系列点组成;图像上每一点坐标(x,y)代表了函数的一对对应值,他的横坐标x表示自变量的某个值,纵坐标y表示与它对应的函数值才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】早晨小欣与妈妈同时从家里出发,步行与自行车向相反方向的两地上学与上班,如图是他们离家的路程![]() 米
米![]() 与时间
与时间![]() 分钟
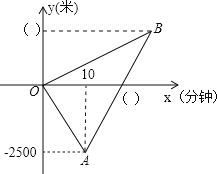
分钟![]() 之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米
之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米![]() 分钟,并且妈妈与小欣同时到达学校
分钟,并且妈妈与小欣同时到达学校![]() 完成下列问题:
完成下列问题:
![]() 在坐标轴两处的括号内填入适当的数据;
在坐标轴两处的括号内填入适当的数据;
![]() 求小欣早晨上学需要的时间.
求小欣早晨上学需要的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,O为坐标原点,抛物线y=a(x﹣h)2﹣4(a>0)与x轴分别交于原点O、A两点,点A在x轴的正半轴上,顶点为D,直线y= ![]() x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.
x交抛物线于B点,过B作BE∥x轴交抛物线另一点E,交对称轴于F.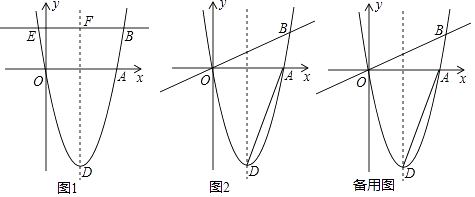
(1)当DF=4a时,求BE的长.
(2)如图2,连AD,连接AD绕点A旋转交直线OB于点G,点D的对应点为G,当OG=2时,求a的值;
(3)在(2)的条件下,当0<a<1时,以OB为直径作圆交x轴下方抛物线于点P,求点P坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
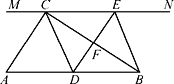
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图a、图b是两张形状、大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,点A、B在小正方形的顶点上.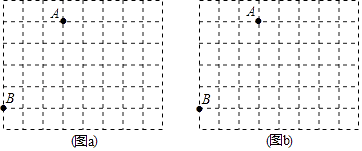
(1)在图a中画出△ABC(点C在小正方形的顶点上),使△ABC是等腰三角形且△ABC为钝角三角形;
(2)在图b中画出△ABD(点D在小正方形的顶点上),使△ABD是等腰三角形,且tan∠ABD=1.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司员工的月工资如下表:
员工 | 经理 | 副经理 | 职员A | 职员B | 职员C | 职员D | 职员E | 职员F | 职员G |
月工资/元 | 4800 | 3500 | 2000 | 1900 | 1800 | 1600 | 1600 | 1600 | 1000 |
则这组数据的平均数、众数、中位数分别为( )
A. 2200元 1800元 1600元 B. 2000元 1600元 1800元
C. 2200元 1600元 1800元 D. 1600元 1800元 1900元
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学学生步行到郊外旅行,七年级![]() 班学生组成前队,步行速度为4千米
班学生组成前队,步行速度为4千米![]() 小时,七
小时,七![]() 班的学生组成后队,速度为6千米
班的学生组成后队,速度为6千米![]() 小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米
小时;前队出发1小时后,后队才出发,同时后队派一名联络员骑自行车在两队之间不间断地来回联络,他骑车的速度为10千米![]() 小时.
小时.
![]() 后队追上前队需要多长时间?
后队追上前队需要多长时间?
![]() 后队追上前队的时间内,联络员走的路程是多少?
后队追上前队的时间内,联络员走的路程是多少?
![]() 七年级
七年级![]() 班出发多少小时后两队相距2千米?
班出发多少小时后两队相距2千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com