Question

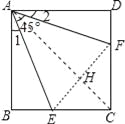
【题目】如图，已知正方形ABCD边长为1，∠EAF=45°，AE=AF，则有下列结论：

①∠1=∠2=22.5°； ②点C到EF的距离是-1； ③△ECF的周长为2； ④BE+DF＞EF．

其中正确的结论是 ．（写出所有正确结论的序号）

Answer 1

【答案】①②③

【解析】试题分析：∵四边形ABCD为正方形， ∴AB=AD，∠BAD=∠B=∠D=90°，

在Rt△ABE和Rt△ADF中， ∴Rt△ABE≌Rt△ADF， ∴∠1=∠2， ∵∠EAF=45°，

∴∠1=∠2=∠22.5°，所以①正确；

连结EF、AC，它们相交于点H，如图，∵Rt△ABE≌Rt△ADF， ∴BE=DF， 而BC=DC， ∴CE=CF，

而AE=AF， ∴AC垂直平分EF，AH平分∠EAF， ∴EB=EH，FD=FH， ∴BE+DF=EH+HF=EF，所以④错误；

∴△ECF的周长=CE+CF+EF=CED+BE+CF+DF=CB+CD=1+1=2，所以③正确；

设BE=x，则EF=2x，CE=1﹣x， ∵△CEF为等腰直角三角形，

∴EF=CE，即2x=（1﹣x），解得x=﹣1， ∴EF=2（﹣1），

∴CH=EF=﹣1，所以②正确．