
【题目】如图,在正方形ABCD中,点E是AB上一动点(不与点A,B重合),点F在AD上,过点E作EG⊥EF交BC于点G,连接FG.
(1)当BE=AF时,求证:EF=EG
(2)若AB=4,AF=1,且设AE=n,
①当FG∥AB时,求n的值;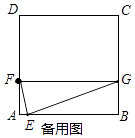
【答案】
(1)
∵四边形ABCD是正方形,
∴∠A=∠B=90°,
∵EG⊥EF,
∴∠AEF+∠BEG=90°,
∵∠AFE+∠AEF=90°,
∴∠AFE=∠BEG,
在△AEF和△BGE中,
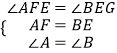 ,
,
∴△AEF≌△BGE(ASA),
∴EF=EG;
(2)
∵FG∥AB,
∴BG=AF=1,
∵AB=4,AE=n,
∴BE=4﹣n,
由(1)可得∠A=∠B=90°,∠AFE=∠BEG,
∴△AEF∽△BGE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴解得n1=2﹣ ![]() ,n2=2+
,n2=2+ ![]() ;
;
②当BG取最大值时,求△EFG的面积.
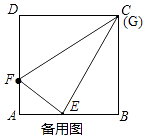
∵△AEF∽△BGE,
∴ ![]() =
= ![]() ,
,
∴BG= ![]() =n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,
=n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,
∴当n=2时,BG有最大值4,
此时点G与点C重合,
∴EF= ![]() =
= ![]() =
= ![]() ,
,
EG= ![]() =
= ![]() =2
=2 ![]() ,
,
∴△EFG的面积= ![]() EG×EF=
EG×EF= ![]() ×
× ![]() ×2
×2 ![]() =5.
=5.
【解析】(1)根据正方形的性质,判定△AEF≌△BGE,即可得出EF=EG;(2)①根据∠A=∠B=90°,∠AFE=∠BEG,即可判定△AEF∽△BGE,进而得到 ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,据此可得n的值;②根据△AEF∽△BGE,得出
,据此可得n的值;②根据△AEF∽△BGE,得出 ![]() =
= ![]() ,即BG=
,即BG= ![]() =n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,进而得到当n=2时,BG有最大值4,据此可得点G与点C重合,再根据勾股定理求得EF=
=n(4﹣n)=﹣n2+4n=﹣(n﹣2)2+4,进而得到当n=2时,BG有最大值4,据此可得点G与点C重合,再根据勾股定理求得EF= ![]() =
= ![]() ,EG=
,EG= ![]() =2
=2 ![]() ,最后根据△EFG的面积=
,最后根据△EFG的面积= ![]() EG×EF进行计算即可.
EG×EF进行计算即可.
【考点精析】本题主要考查了全等三角形的性质和相似三角形的性质的相关知识点,需要掌握全等三角形的对应边相等; 全等三角形的对应角相等;对应角相等,对应边成比例的两个三角形叫做相似三角形才能正确解答此题.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
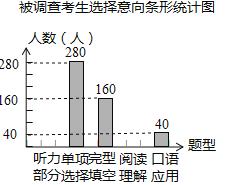
【题目】为了解中考考生最喜欢做哪种类型的英语客观题,2015年志愿者奔赴全市中考各考点对英语客观题的“听力部分、单项选择、完型填空、阅读理解、口语应用”进行了问卷调查,要求每位考生都自主选择其中一个类型,为此随机调查了各考点部分考生的意向.并将调查结果绘制成如图的统计图表(问卷回收率为100%,并均为有效问卷).
被调查考生选择意向统计表

根据统计图表中的信息,解答下列问题:
(1)求本次被调查的考生总人数及a、b、c的值;
(2)将条形统计图补充完整;
(3)全市参加这次中考的考生共有42000人,试估计全市考生中最喜欢做“单项选择”这类客观题的考生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线a经过正方形ABCD的顶点A,分别过正方形的顶点B、D作BF⊥a于点F,DE⊥a于点E,若DE=8,BF=5,则EF的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AD长为6,AB是弦,∠A=30°,CD∥AB,且CD= ![]() .
. 
(1)求∠C的度数;
(2)求证:BC是⊙O的切线;
(3)求阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“美丽抚顺”的工作部署,市政府计划对城区道路进行了改造,现安排甲、乙两个工程队完成.已知甲队的工作效率是乙队工作效率的![]() 倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
倍,甲队改造360米的道路比乙队改造同样长的道路少用3天.
(1)甲、乙两工程队每天能改造道路的长度分别是多少米?
(2)若甲队工作一天需付费用7万元,乙队工作一天需付费用5万元,如需改造的道路全长1200米,改造总费用不超过145万元,至少安排甲队工作多少天?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人参加某体育项目训练,为了便于研究,把最后5次的训练成绩分别用实线和虚线连接起来,如图,下面的结论错误的是( )
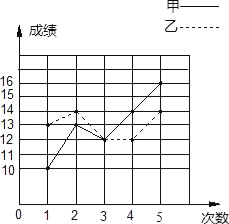
A. 乙的第2次成绩与第5次成绩相同
B. 第3次测试,甲的成绩与乙的成绩相同
C. 第4次测试,甲的成绩比乙的成绩多2分
D. 在5次测试中,甲的成绩都比乙的成绩高
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在每个小正方形的边长为 ![]() 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距
的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距 ![]() 的另一个格点的运动称为一次跳马变换.例如,在
的另一个格点的运动称为一次跳马变换.例如,在 ![]() 的正方形网格图形中(如图1),从点
的正方形网格图形中(如图1),从点 ![]() 经过一次跳马变换可以到达点
经过一次跳马变换可以到达点 ![]() ,
, ![]() ,
, ![]() ,
, ![]() 等处.现有
等处.现有 ![]() 的正方形网格图形(如图2),则从该正方形的顶点
的正方形网格图形(如图2),则从该正方形的顶点 ![]() 经过跳马变换到达与其相对的顶点
经过跳马变换到达与其相对的顶点 ![]() ,最少需要跳马变换的次数是( )
,最少需要跳马变换的次数是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com