
分析 根据a>0,b>a+c判断一元二次方程的根的判别式△的符号即可.
解答 解:∵a>0,b>a+c,△=b2-4ac,
①当c>0时,
∴△=b2-4ac>(a+c)2-4ac=a2+c2-2ac=(a-c)2≥0.
即△>0,
∴方程有两个不相等的实数根.
②当c<0时,
∵a>0,
∴ac<0
∴△=b2-4ac>0,
∴方程有两个不相等的实数根.
③c=0时,∵b>a+c,
∴△>0,
∴方程有两个不相等的实数根.
综上所述方程有两个不相等的实数根.
点评 本题主要考查了根的判别式的知识,解答本题的关键是要掌握一元二次方程根的情况与判别式△的关系:△>0?方程有两个不相等的实数根;△=0?方程有两个相等的实数根;△<0?方程没有实数根.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
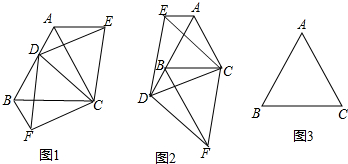
 如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,图中点D、点E、点F也都在格点上,则下列与△ABC相似的三角形是( )
如图,在8×4的矩形网格中,每格小正方形的边长都是1,若△ABC的三个顶点在图中相应的格点上,图中点D、点E、点F也都在格点上,则下列与△ABC相似的三角形是( )| A. | △ACD | B. | △ADF | C. | △BDF | D. | △CDE |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
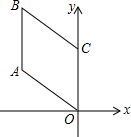 如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )
如图,四边形OABC是菱形,若OA=2,∠AOC=45°,则B点的坐标是 ( )| A. | (-2,2+$\sqrt{2}$) | B. | (2,2+$\sqrt{2}$) | C. | ($-\sqrt{2}$,2+$\sqrt{2}$) | D. | ($\sqrt{2}$,2+$\sqrt{2}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
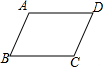 如图所示,四边形ABCD是平行四边形.
如图所示,四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正比例函数 | B. | 一次函数 | C. | 反比例函数 | D. | 二次函数 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
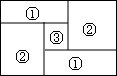 如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com