Question

20．已知△ABC为等边三角形，D为AB边所在的直线上的动点，连接DC，以DC为边在DC两侧作等边△DCE和等边△DCF（点E在DC的右侧或上侧，点F在DC左侧或下侧），连接AE、BF
（1）如图1，若点D在AB边上，请你通过观察，测量，猜想线段AE、BF和AB有怎样的数量关系？并证明你的结论；
（2）如图2，若点D在AB的延长线上，其他条件不变，线段AE、BF和AB有怎样的数量关系？请直接写出结论（不需要证明）；
（3）若点D在AB的反向延长线上，其他条件不变，请在图3中画出图形，探究线段AE、BF和AB有怎样的数量关系，并直接写出结论（不需要证明）

Answer 1

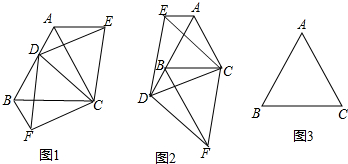
分析 （1）AE+BF=AB，可证明△CBF≌△CAD和△CDB≌△CAE分别得到AD=BF，BD=AE，易得结论；
（2）BF-AE=AB，由△CBF≌△CAD和△CBD≌△CAE分别得到AD=BF，BD=AE，易得结论；
（3）AE-BF=AB，由△CBF≌△CAD和△CBD≌△CAE分别得到AD=BF，BD=AE，易得结论．

解答 解：（1）AE+BF=AB，如图1，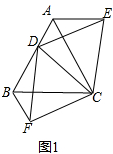
∵△ABC和△DCF是等边三角形，
∴CA=CB，CD=CF，∠ACB=∠DCF=60°．
∴∠ACD=∠BCF，
在△ACD和△BCF中
$\left\{\begin{array}{l}{CA=CB}\\{∠ACD=∠BCF}\\{CD=CF}\end{array}\right.$
∴△ACD≌△BCF（SAS）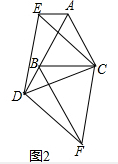
∴AD=BF
同理：△CBD≌△CAE（SAS）
∴BD=AE
∴AE+BF=BD+AD=AB；
（2）BF-AE=AB，
如图2，易证△CBF≌△CAD和△CBD≌△CAE，
∴AD=BF，BD=AE，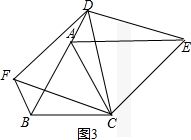
∴BF-AE=AD-BD=AB；
（3）AE-BF=AB，
如图3，易证△CBF≌△CAD和△CBD≌△CAE，
∴AD=BF，BD=AE，
∴BF-AE=AD-BD=AB．

点评 本题主要考查了三角形全等的判定与性质，灵活运用类比思想，在变化中发现不变是解决问题的关键．