
分析 (1)先把抛物线解析式化为一般式,再计算△的值,得到△=1>0,于是根据△=b2-4ac决定抛物线与x轴的交点个数即可判断不论m为何值,该抛物线与x轴一定有两个公共点;
(2)①根据对称轴方程得到=-$\frac{-(2m+1)}{2}$=$\frac{5}{2}$,然后解出m的值即可得到抛物线解析式;
②根据抛物线的平移规律,设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2-5x+6+k,再利用抛物线与x轴的只有一个交点得到△=52-4(6+k)=0,
然后解关于k的方程即可.
解答 (1)证明:y=(x-m)2-(x-m)=x2-(2m+1)x+m2+m,
∵△=(2m+1)2-4(m2+m)=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)解:①∵x=-$\frac{-(2m+1)}{2}$=$\frac{5}{2}$,
∴m=2,
∴抛物线解析式为y=x2-5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2-5x+6+k,
∵抛物线y=x2-5x+6+k与x轴只有一个公共点,
∴△=52-4(6+k)=0,
∴k=$\frac{1}{4}$,
即把该抛物线沿y轴向上平移$\frac{1}{4}$个单位长度后,得到的抛物线与x轴只有一个公共点.
点评 本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
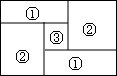 如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )
如图,小明家的住房平面图呈长方形,被分割成3个正方形和2个长方形后仍是中心对称图形.若只知道原住房平面图长方形的周长,则分割后不用测量就能知道周长的图形的标号为( )| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.1×10-8s | B. | 0.1×10-9s | C. | 1×10-8s | D. | 1×10-9s |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 过直线外一点可以画无数条直线与这条直线垂直 | |
| B. | 过直线外一定点不可以画这条直线的垂线 | |
| C. | 过直线外一点可以画这条直线的一条垂线 | |
| D. | 如果两条直线不相交,那么这两条直线有可能互相垂直 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com