
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:解答题
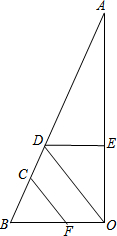 如图,完成下列推理过程
如图,完成下列推理过程查看答案和解析>>
科目:初中数学 来源: 题型:解答题
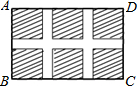 如图,小区计划在一个长为40cm,宽为26m的矩形场地ABCD上修建三条同样宽的路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144m2,求路的宽度.
如图,小区计划在一个长为40cm,宽为26m的矩形场地ABCD上修建三条同样宽的路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144m2,求路的宽度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
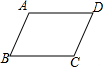 如图所示,四边形ABCD是平行四边形.
如图所示,四边形ABCD是平行四边形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
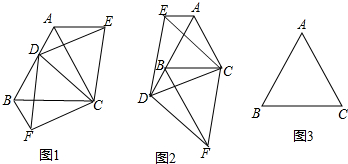
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
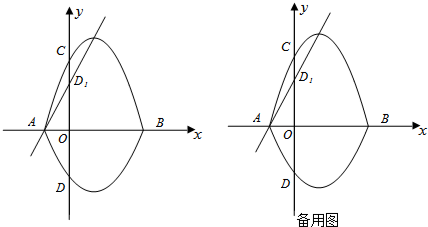
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com