
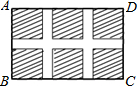
 如图,小区计划在一个长为40cm,宽为26m的矩形场地ABCD上修建三条同样宽的路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144m2,求路的宽度.
如图,小区计划在一个长为40cm,宽为26m的矩形场地ABCD上修建三条同样宽的路,使其中两条与AB平行,另一条与AD平行,其余部分种草,若使每一块草坪的面积都为144m2,求路的宽度. 分析 设小路的宽为xm,那么小路所占面积为(40x+2×26x-2x2),于是六块草坪的面积为[40×26-(40x+2×26x-2x2)],根据面积之间的关系可列方程40×26-(40x+2×26x-2x2)=144×6,解方程求解,并根据实际意义进行值的取舍即可确定甬路的宽.
解答 解:设小路的宽为xm,根据题意得40×26-(40x+2×26x-2x2)=144×6,
整理得x2-46x+88=0,
解得x1=44,x2=2,
当x=44时不符合题意,故舍去,
所以x=2.
答:路的宽度是2m.
点评 本题考查的是一元二次方程的应用以及矩形面积计算公式,难度一般.找到关键描述语,找到等量关系准确的列出方程是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )
如图,在?ABCD中,AB=6,AD=8,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE于G,BG=4$\sqrt{2}$,则四边形AECD的周长为( )| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).
南水北调工程中线已经在12月27日开始向北京、天津等地供水.为了进一步加强居民的节水意识,合理调配水资源,某区决定对本区的居民用水实行额定用水管理.为了更好的确定额定用水的用水量,首先对本区居民的目前生活用水量进行了入户调查.下表是通过简单随机抽样获得的50个家庭去年的月均用水量(单位:吨).| 分组 | 划记(用正字划记) | 频数 |
| 2.0<x≤3.5 | ||
| 3.5<x≤5.0 | ||
| 5.0<x≤6.5 | ||
| 6.5<x≤8.0 | ||
| 8.0<x≤9.5 | ||
| 合计 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
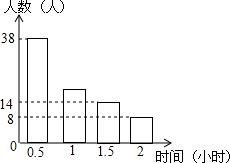 随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:
随着“微信”的流行,不少初中学生在微信朋友圈忙着“发状态”,某校在使用微信的学生中随机抽取了部分,并调查他们平常每天上微信的时间,绘制了统计表和条形统计图:| 上微信的时间(小时) | 频数(人数) | 频率 |
| 0.5 | 38 | a |
| 1 | b | 0.25 |
| 1.5 | 14 | c |
| 2 | 8 | 0.1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com