
有一种传染性疾病,蔓延速度极快.据统汁,在人群密集的某城市里,通常情况下,每人一天能传染给若干人,通过计算解答下面的问题:
(1)现有一人患了这种疾病,开始两天共有225人患上此病,求每天一人传染了几人?
(2)两天后,人们有所觉察,这样平均一 个人一天以少传播5人的速度在递减,求再过两天共有多少人患有此病?
个人一天以少传播5人的速度在递减,求再过两天共有多少人患有此病?
【考点】一元二次方程的应用.
【专题】应用题.
【分析】(1)第一天患病的人数为1+1×传播的人数;第一天患病人数将成为第二天的传染源,第二天患病的人数为第一天患病的人数×传播的人数,等量关系为:第一天患病的人数+第二天患病的人数=225;
(2)再过两天的患病人数=225+225×(原来的传播人数﹣5)+前3天一共患病的人数×(第3天的传播人数﹣5).
【解答】解:(1)设每天一人传染了x人.
1+x+(1+x)×x=225,
(1+x)2=225,
∵1+x>0,
∴1+x=15,
x=14.
答:每天一人传染了14人;
(2)再过两天的患病人数=225+225×(14﹣5)+[225+225×(14﹣5)]×(14﹣5﹣5)=11250.
答:共有11250人患病.
【点评】考查一元二次方程的应用;得到两天患病人数的等量关系是解决本题的关键;易错点是理解第一天患病的总人数是第二天的传染源.


科目:初中数学 来源: 题型:
小米将两块相同的三角板摆成如图1的形状,三角板的斜边长为10cm,较小锐角为30°,点B、C、F、D在同一条直线上,且点C与点F重合,小米在对这两块三角板进行如下操作时遇到了如下问题,请你帮助他解决.
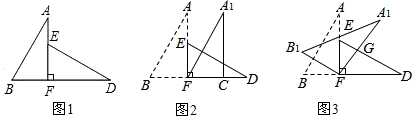
(1)将图1中的△ABC沿BD向右平移到图2的位置,使点B与点C重合,求出平移的距离;
(2)将图1中的△ABC绕点C顺时针方向旋转30°到图3的位置,A、C交DE于点G,求出线段GC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
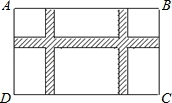
如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为570米2,问小路应为多宽?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com