练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    若（m+1）x2+2mx﹣1=0是关于x的一元二次方程，则m的值是__________．


    是m≠﹣1．

    【考点】根的判别式．

    【分析】一元二次方程必须满足两个条件：（1）未知数的最高次数是2；（2）二次项系数不为0．由这两个条件得到相应的关系式m+1≠0，再解不等式，进一步结合根的判别式判定即可．

    【解答】解：由题意得：m+1≠0，

    解得：m≠﹣1，

    且△=b2﹣4ac=4m2+4（m+1）=（2m+1）2+3＞0，

    方程始终有两个不相等的实数根．

    故答案为：m≠﹣1．

    【点评】此题主要考查了一元二次方程的概念．只有一个未知数且未知数最高次数为2的整式方程叫做一元二次方程，一般形式是ax2+bx+c=0（且a≠0）．特别要注意a≠0的条件．以及根的判别式．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    解方程：．

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图所示，在平面直角坐标系中，点A、B的坐标分别为（﹣2，0）和（2，0）．月牙①绕点B顺时针旋转90°得到月牙②，则点A的对应点A′的坐标为(     )

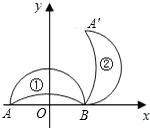
    A．（2，2）   B．（2，4）   C．（4，2）   D．（1，2）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在⊙O中，弦AD、BC相交于点E，连结OE，已知=．

    （1）求证：BE=DE；

    （2）如果⊙O的半径为5，AD⊥CB，DE=1，求AE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知二次函数y=kx2﹣5x﹣5的图象与x轴有交点，则k的取值范围是(     )

    A．  B．且k≠0       C．  D．且k≠0

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知抛物线y=ax2+bx+c（a＞0）的对称轴为直线x=1，且经过点（﹣1，y1），（2，y2），试比较y1和y2的大小：y1__________y2．（填“＞”，“＜”或“=”）

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    有一种传染性疾病，蔓延速度极快．据统汁，在人群密集的某城市里，通常情况下，每人一天能传染给若干人，通过计算解答下面的问题：

    （1）现有一人患了这种疾病，开始两天共有225人患上此病，求每天一人传染了几人？

    （2）两天后，人们有所觉察，这样平均一个人一天以少传播5人的速度在递减，求再过两天共有多少人患有此病？

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    若，则a的取值范围是__________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    某产品生产车间有工人10名．已知每名工人每天可生产甲种产品12个或乙种产品10个，且每生产一个甲种产品可获得利润100元，每生产一个乙种产品可获得利润180元．在这10名工人中，车间每天安排x名工人生产甲种产品，其余工人生产乙种产品．

    （1）请写出此车间每天获取利润y（元）与x（人）之间的函数关系式；

    （2）若要使此车间每天获取利润为14400元，要派多少名工人去生产甲种产品？

    （3）若要使此车间每天获取利润不低于15600元，你认为至少要派多少名工人去生产乙种产品才合适？

    查看答案和解析>>

    同步练习册答案