
已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(﹣1,y1),(2,y2),试比较y1和y2的大小:y1__________y2.(填“>”,“<”或“=”)
科目:初中数学 来源: 题型:
如图13-1,为美化校园环境,某校计划在一块长为60米,宽为40米的长方形空地上修建一个长方形花圃,并将花圃四周余下的空地修建成同样宽的通道,设通道宽为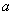 米.
米.
(1)用含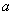 的式子表示花圃的面积;
的式子表示花圃的面积;
(2)如果通道所占面积是整个长方形空地面积的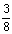 ,求出此时通道的宽;
,求出此时通道的宽;
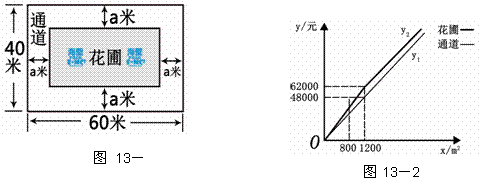
(3)已知某园林公司修建通道、花圃的造价 (元)、
(元)、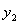 (元)与修建面积
(元)与修建面积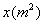 之间的函数关系如图13-2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?
之间的函数关系如图13-2所示,如果学校决定由该公司承建此项目,并要求修建的通道的宽度不少于2米且不超过10米,那么通道宽为多少时,修建的通道和花圃的总造价最低,最低总造价为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )

A.ac+1=b B.ab+1=c C.bc+1=a D.以上都不是
查看答案和解析>>
科目:初中数学 来源: 题型:
三角形两边的长分别是8和6,第三边的长是方程x2﹣12x+20=0的一个实数根,则此三角形的周长是( )
A.24 B.24或16 C.16 D.22
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com