
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )

A.ac+1=b B.ab+1=c C.bc+1=a D.以上都不是
A【考点】二次函数图象与系数的关系.
【专题】数形结合.
【分析】根据图象易得C(0,c)且c>0,再利用OA=OC可得A(﹣c,0),然后把A(﹣c,0)代入y=ax2+bx+c即可得到a、b、c的关系式.
【解答】解:当x=0时,y=ax2+bx+c=c,则C(0,c)(c>0),
∵OA=OC,
∴A(﹣c,0),
∴a•(﹣c)2+b•(﹣c)+c=0,
∴ac﹣b+1=0,
即ac+1=b.
故选A.
【点评】本题考查了二次项系数与系数的关系:对于二次函数y=ax2+bx+c(a≠0),二次项系数a决定抛物线的开口方向和大小:当a>0时,抛物线向上开口;当a<0时,抛物线向下开口;一次项系数b和二次项系数a共同决定对称轴的位置:当a与b同号时(即ab>0),对称轴在y轴左; 当a与b异号时(即ab<0),对称轴在y轴右.(简称:左同右异);常数项c决定抛物线与y轴交点:抛物线与y轴交于(0,c);抛物线与x轴交点个数由△决定:△=b2﹣4ac>0时,抛物线与x轴有2个交点;△=b2﹣4ac=0时,抛物线与x轴有1个交点;△=b2﹣4ac<0时,抛物线与x轴没有交点.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
某商场要经营一种新上市的文具,进价为20元/件,试营销阶段发现;当销售单价为25元/件时,每天的销售量是250件,销售单价每上涨1元,每天的销售量就减少10件.
(1)写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;
(2)当销售单价为多少时,该文具每天的销售利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,在平面直角坐标系中,点A、B的坐标分别为(﹣2,0)和(2,0).月牙①绕点B顺时针旋转90°得到月牙②,则点A的对应点A′的坐标为( )
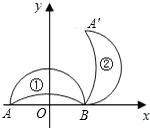
A.(2,2) B.(2,4) C.(4,2) D.(1,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知抛物线y=ax2+bx+c(a>0)的对称轴为直线x=1,且经过点(﹣1,y1),(2,y2),试比较y1和y2的大小:y1__________y2.(填“>”,“<”或“=”)
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别是从A,B同时出发,求:
(1)经过多少时间,△PBQ的面积等于8cm2?
(2)经过多少时间,五边形APQCD的面积最小,最小值是多少?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com