
如图,矩形ABCD中,AB=6cm,BC=12cm,点P从A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别是从A,B同时出发,求:
(1)经过多少时间,△PBQ的面积等于8cm2?
(2)经过多少时间,五边形APQCD的面积最小,最小值是多少?

【考点】二次函数综合题;矩形的性质.
【专题】动点型.
【分析】(1)设运动时间为t,根据P、Q运动的速度及AB、BC的长求出t的取值范围,根据三角形的面积公式即可求解.
(2)设运动时间为t,△PBQ的面积最大时,五边形APQCD的面积最小,求出t的值即可.
【解答】解:(1)设运动时间为t,则PB=6﹣t,BQ=2t,
则S△PBQ=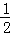 PB•BQ=
PB•BQ=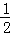 ×(6﹣t)×2t=8,
×(6﹣t)×2t=8,
解得t=2或t=4,
故经过2秒或4秒时,△PBQ的面积等于8cm2.
(2)根据(1)中所求出的S△PBQ=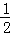 PB•BQ=
PB•BQ=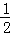 ×(6﹣t)×2t,
×(6﹣t)×2t,
整理得S△PBQ=﹣t2+6t.
当t=﹣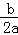 =3时,S△PBQ最大=
=3时,S△PBQ最大=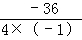 =9,
=9,
故S五边形APQCD=S矩形ABCD﹣S△PBQ最大=6×12﹣9=63cm2.
故当t=3秒,五边形APQCD的面积最小,最小值是63cm2
【点评】此题是典型的动点问题,涉及到矩形及三角形的面积公式,二次函数的最值问题,比较简单


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
二次函数y=ax2+bx+c的图象如图,点C在y轴的正半轴上,且OA=OC,则( )

A.ac+1=b B.ab+1=c C.bc+1=a D.以上都不是
查看答案和解析>>
科目:初中数学 来源: 题型:
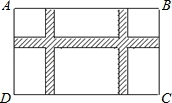
如图,某小区规划在长32米,宽20米的矩形场地ABCD上修建三条同样宽的3条小路,使其中两条与AD平行,一条与AB平行,其余部分种草,若使草坪的面积为570米2,问小路应为多宽?
查看答案和解析>>
科目:初中数学 来源: 题型:
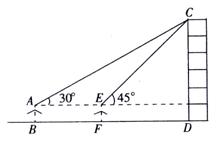
小敏同学测量一建筑物CD的高度,她站在B处仰望楼顶C,测得仰角为30°,再往建筑物方向走30m,到达点 F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据:
F处测得楼顶C的仰角为45°(B,F,D在同一条直线上)。一直小敏的眼睛与地面距离为1.5m,求这栋建筑物CD的高度(参考数据: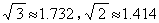 ,结果保留整数)
,结果保留整数)
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com